 拆点
拆点
# 拆点
拆点不是一种具体算法,而是一种图论中的重要思想,样用于网络流,用来处理点权或者点的流量限制问题,也适用于分层图
# 结点有流量限制的最大流
把一个节点 拆成两个节点 然后 承载别的连到这个点的边, 往别的节点练边
原图是这样的
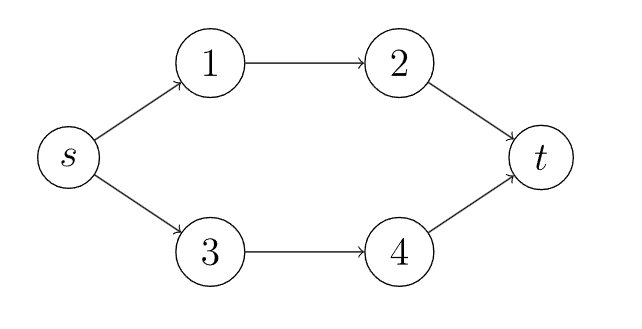
拆点后是这样的
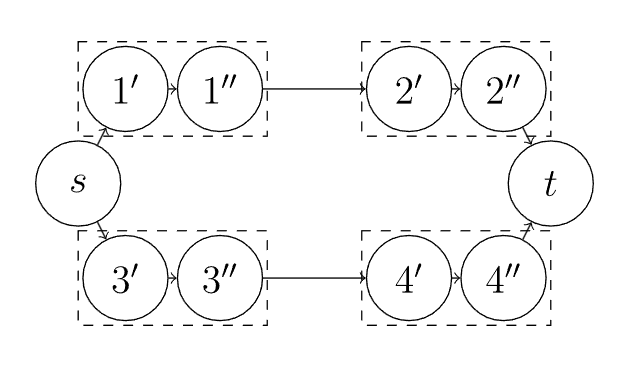
# 分层图最短路
看一个例题
洛谷 P4568「JLOI2011」飞行路线 (opens new window)
有 次零代价通过一条路径,求总的最小花费
我们可以采用 DP 思想,定义 表示从起点到 ,使用看 次免费通行权限后的最短路径,显然转移方程为
其中 为 的父节点, 为这条路的边权,当 时,
实际上,这个 DP 就相当于把每个节点拆成了 个节点,然后在分层图上跑最短路
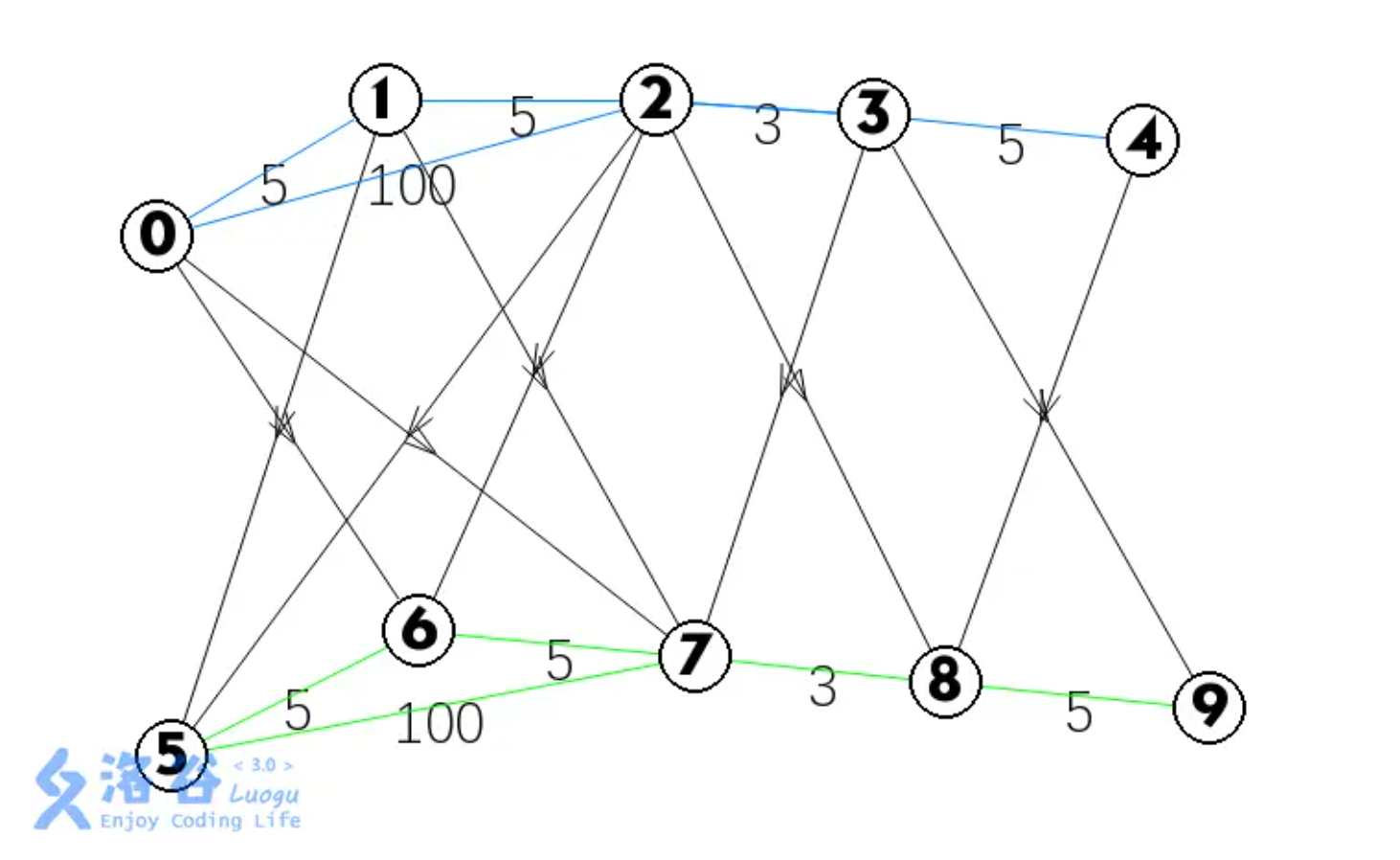
上次更新: 2025/04/08, 18:03:31
