二分图

定义

• 节点由两个集合组成
• 两个集合内部没有边的图

换言之，存在一种方案，将节点划分成满足以上性质的两个集合

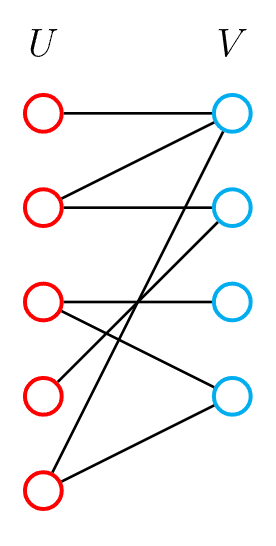
如果两个集合中的点分别染成黑色和白色，可以发现二分图中的每一条边都一定是连接一个黑色点和一个白色点

二分图不存在长度为奇数的环

为什么？因为每一条边都是从一个集合走到另一个集合，只有走偶数次才可能走到同一个集合

判定一个图是否为二分图

DFS 和 BFS 判断有没有奇数环即可

二分图最大匹配

给定一个二分图 $G$ ，即左右两部分，各部分之间的点没有边连接，要求选出一些边，使得这些边没有公共顶点，且边的数量最大。

换作夫妻匹配问题，就是问在一夫一妻制下最多能找到多少对夫妻

著名的解决二分图最大匹配问题的算法为匈牙利算法，也可以借助最大流/最小割模型解决这类问题

匈牙利算法

匈牙利算法是基于深度优先搜索一遍一遍搜索增广路的存在性来增加匹配对数的

因为增广路长度为奇数，路径起始点非左即右，所以我们先考虑从左边的未匹配点找增广路。 注意到因为交错路的关系，增广路上的第奇数条边都是非匹配边，第偶数条边都是匹配边，于是左到右都是非匹配边，右到左都是匹配边。

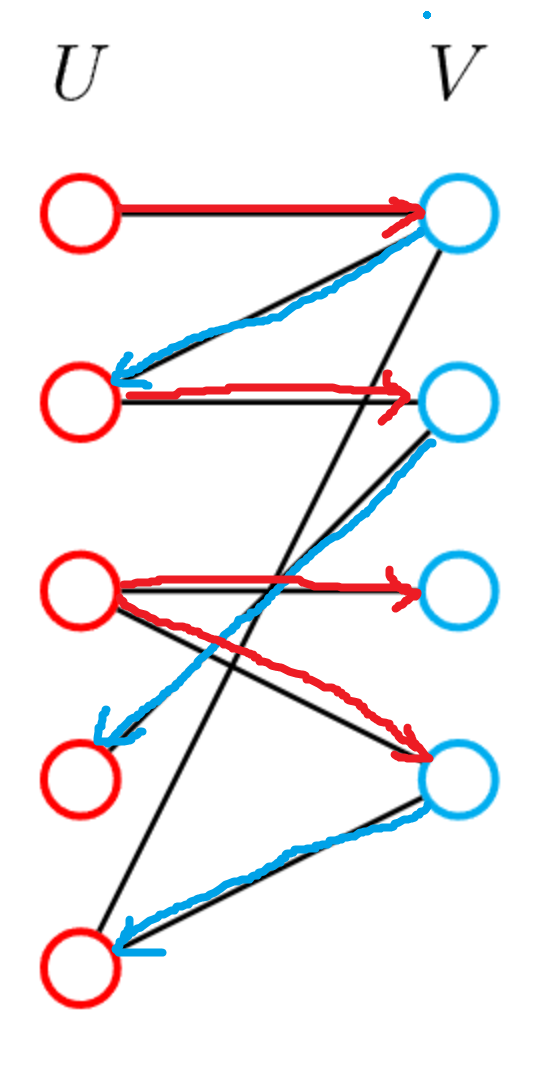
图中，红色的是非匹配边，蓝色的是匹配边

于是我们给二分图 定向，问题转换成，有向图中从给定起点找一条简单路径走到某个未匹配点，此问题等价给定起始点 $s$ 能否走到终点 $t$。 那么只要从起始点开始 DFS 遍历直到找到某个未匹配点。 未找到增广路时，我们拓展的路也称为 交错树。

找到未匹配点之后，我们回溯时修改匹配，

---

另外一种理解

我们将问题看作相亲现场，每个 $U$ 集合的人排队寻找 $V$ 集合里的对象

假设是男生排队找女生，基于这个"时间"顺序，假设前面的男生已经匹配了一些

下一个男生 $a$ 进来匹配，算法便会遍历一遍他认识的女生（与他有关系的 $V$ 集内的点）

如果发现当前遍历到的女生还没有被其他男生匹配，那非常好，就直接把这个女生匹配给男生 $a$

如果发现已经被其他男生 $b$ 给匹配了，那算法会尝试去和那个男生 $b$ 沟通，询问能否让他换一个（？）

算法便会来到那个男生 $b$ 那里，重新遍历一遍他认识的女生，看看能否找到其他能够匹配的女生（寻找增广路/套娃）

• 如果可以，那么男生 $b$ 便会与新找到的女生匹配，顺利成章的，原来与男生 $b$ 匹配的女生就可以和男生 $a$ 匹配啦
• 如果不行，那么男生 $a$ 就没这个机会了QAQ，尝试下一个吧（继续遍历），实在不行（遍历完了）单着挺好的

就以这样的方法一直搜索，直到所有男生（$U$ 集）该匹配的都匹配完了，就能得到最大匹配数了

复杂度

因为要枚举 $n$ 个点，总复杂度为 $O(nm)$

#include <bits/stdc++.h>
using namespace std;
int main() {
    freopen ("P3386.in", "r", stdin);
    int n, m, e; cin >> n >> m >> e;
    vector<vector<int>> g(n + m + 1);
    vector<int> vis(n + m + 1, 0), match(n + m + 1, 0);
    for (int i = 1; i <= e; i++) {
        int x, y; cin >> x >> y;
        g[x].push_back(y + n);
        g[y + n].push_back(x);
    }
    int ans = 0;

    auto dfs = [&] (auto &&dfs, int u) -> bool  {
        for (int v : g[u]) {
            if (vis[v]) continue;
            vis[v] = 1;
            if (!match[v] || dfs(dfs, match[v])) { //如果没有被匹配或者 和son匹配的那个点 可以找到新的点匹配，那么son就和x匹配
                match[u] = v;
                match[v] = u;
                return true;
            }
        }
        return false;
    };

    for (int i = 1; i <= n; i++) {
        if (!match[i]) {
            fill(vis.begin(), vis.end(), 0);
            if (dfs(dfs, i)) ans++;
        }
    }
    cout << ans << endl;
    return 0;
}

转化成最大流

由于一个点最多可以匹配到一条边，每条边又表示着两点间存在关系，所以可以建立一个超级原点 $S$ 和超级汇点 $T$

将 $S$ 与 $U$ 集合每个点建立一条边，流量为 $1$，表示每个人最多只能被 $1$ 条边匹配，同理，$V$ 集合中的每个点与 $T$ 建立一条边，流量为 $1$。最后，如果 $U$ 集中的点 $a$ 与 $V$ 集中的点 $b$ 可以匹配，那么建立一条 $a$ 到 $b$ 的边，流量也为 $1$

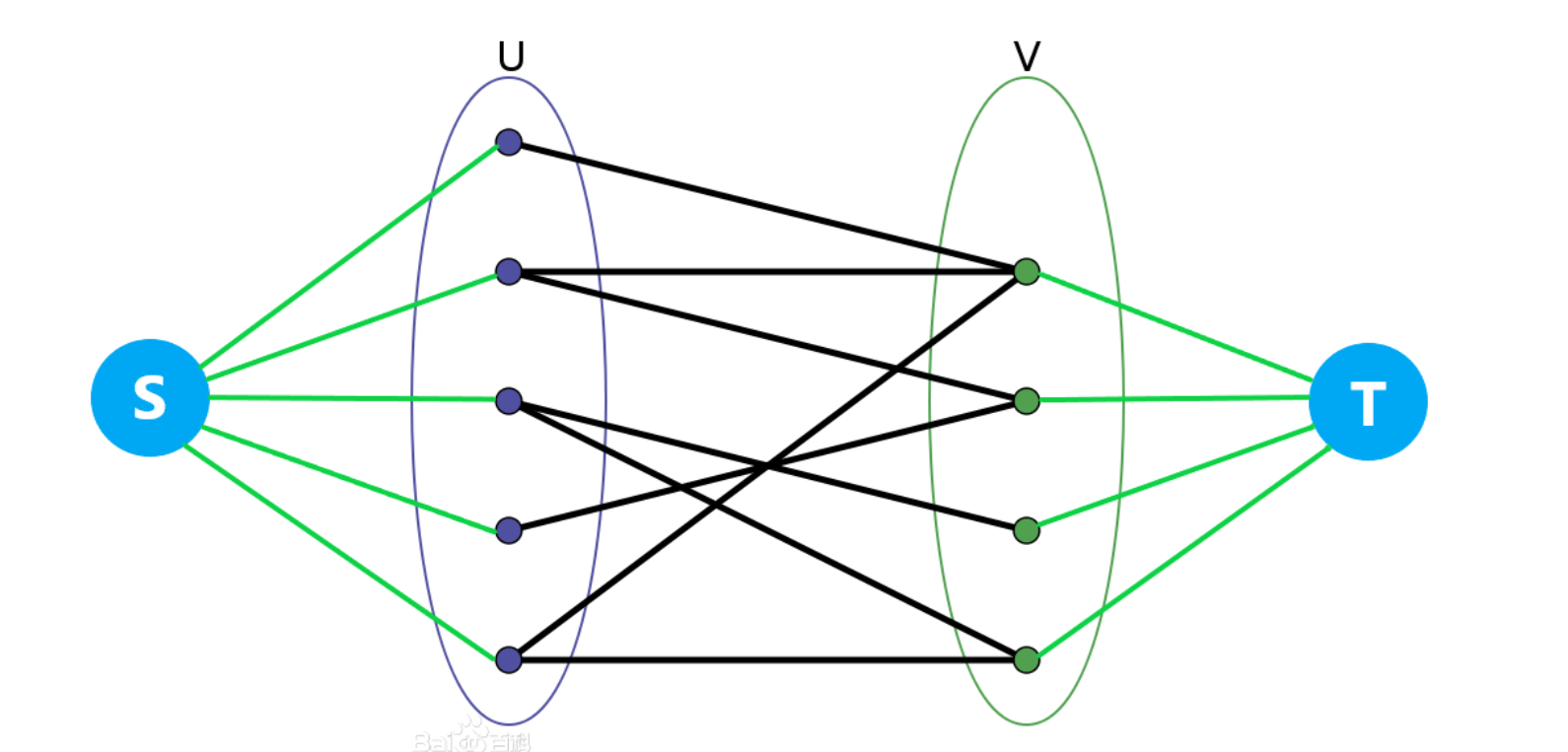
这样最大流 = 二分图的最大匹配

洛谷 P3386 【模板】二分图最大匹配 (opens new window)

#include <bits/stdc++.h>
using namespace std;

const int INF = 0x3f3f3f3f;

struct Dinic {
    struct Edge {
        int from, to, cap, flow;
    };
    int n, m, s, t;
    vector<Edge> edges;
    vector<vector<int>> g;
    vector<int> d, cur; // d 为层次，cur 为当前弧优化

    void init (int n_) {
        n = n_; edges.clear();
        d.assign(n, 0);
        g.assign(n, vector<int>());
    }

    void add_e (int from, int to, int cap) {
        edges.push_back(Edge{from, to, cap, 0});
        edges.push_back(Edge{to, from, 0, 0});
        m = edges.size();
        g[from].push_back(m - 2);
        g[to].push_back(m - 1);
    }

    bool bfs () {
        vector<int> vis (n, 0);
        queue<int> q; q.push(s); d[s] = 0; vis[s] = 1;
        while (!q.empty()) {
            int x = q.front(); q.pop();
            for (auto i : g[x]) {
                Edge &e = edges[i];
                if (vis[e.to] == 0 && e.cap > e.flow) {
                    vis[e.to] = 1;
                    d[e.to] = d[x] + 1;
                    q.push(e.to);
                }
            }
        }
        return vis[t]; // 是否存在能到达汇点的路径
    }

    int dfs (int x, int a) { // a 表示从源点到 x 的可改进量
        if (x == t || a == 0) return a;
        int flow = 0, f;
        for (int &i = cur[x]; i < g[x].size(); i++) { // 当前弧优化，在 cur[x] 之前都没有增广成功
            Edge &e = edges[g[x][i]];
            if (d[x] + 1 == d[e.to] && (f = dfs(e.to, min(a, e.cap - e.flow))) > 0) {
                e.flow += f;
                edges[g[x][i] ^ 1].flow -= f;
                flow += f;
                a -= f;
                if (a == 0) break;
            }
        }
        return flow;
    }

    int max_flow (int s, int t) {
        this->s = s; this->t = t;
        int flow = 0;
        while (bfs()) {
            cur.assign(n, 0);
            flow += dfs(s, INF);
        }
        return flow;
    }
};


int main() {
    int n, m, e; cin >> n >> m >> e;
    Dinic dinic; dinic.init(n + m + 2);
    int S = 0, T = n + m + 1;
    for (int i = 1; i <= e; i++) {
        int x, y; cin >> x >> y;
        dinic.add_e(x, y + n, 1);
    }
    for (int i = 1; i <= n; i++) dinic.add_e(S, i, 1);
    for (int i = 1; i <= m; i++) dinic.add_e(i + n, T, 1);
    auto ans = dinic.max_flow(S, T);
    cout << ans << endl;
    return 0;

}

二分图最大权完美匹配

二分图最大权完美匹配，表示此时的二分图的边是带有边权的

与二分图最大匹配不同的是，最大权完美匹配侧重于最大权值，要求在保证一个点最多只能有与其有关系的一条边被选中的前提下，选出的边的边权总和最大

换做夫妻匹配问题，同样以一夫一妻制为背景，但此时男女生之间存在一种叫好感度的数值，要求好感度总和最大

著名的解决二分图最大权完美匹配问题的算法为 KM算法

KM 算法

km算法的核心思路在于：

• 定义顶标 $lx[i],ly[i]$，则对于一条边，都有性质 $lx[u]+ly[v] \ge e[u][v]$
• 当且仅当 $lx[u]+ly[v]=e[u][v]$ 时，我们称该边为 相等边
• 所有点和所有相等边所组成的子图称为相等子图
• 核心算法：贪心地将増广所需的边中，边权最大的那些边变成相等边，即逐渐扩大相等子图
• 核心性质：扩大相等子图至其刚好有完美匹配时，该匹配即为原图的最大权完美匹配（很好理解，因为扩大相等子图的过程是贪心的）

由此，我们便能将km算法简单地理解为：匈牙利算法+扩大相等子图

顶标的设计是 km 的精髓

• $lx[i]$ 为左部点的顶标
• $ly[i]$ 为右部点的顶标
• $vx[i]$ 左部点遍历标记
• $vy[i]$ 右部点遍历标记
• $px[i]$ 左部点匹配
• $py[i]$ 右部点匹配
• $slack[i]$ 对于指向右部点 $i$ 的所有边 $\min(lx[u]+ly[i]-e[u][i])$ 的值，即松弛量 （初始化为 $INF$），当 $slack[i]==0$ 时，表示对于右部点 $i$ ，相等子图中有一条指向它的边

初始时，我们要保证 $lx[u]+ly[v]\ge e[u][v]$ ，一般，我们把 $lx[u]$ 设为和 $u$ 连边最大的 $e[u][v]$ ，$ly[v]$ 设为 $0$

需要补全虚边，设置为 $-INF$

修改顶标的思路可以具体看代码，核心语句如下（copy的是下面 bfs 正解的过程）：

if(vx[i]) lx[i]-=d;
if(vy[i]) ly[i]+=d; else slack[i]-=d;

这样修改的目的是保证已在相等子图中的边两侧顶标和不变，同时通过左部点顶标的减小实现向相等子图中拉近相等边的目的

对于原图中的某条边：

1. $vx[u]=0,vy[v]=0$ ，$slack[v]$ 不变（未遍历到的=>不修改）
2. $vx[u]=1,vy[v]=1$ ，$slack[v]$ 不变（已遍历到的=>该边为相等边=>修改后依旧为相等边）
3. $vx[u]=0,vy[v]=1$ ，则 $slack[v]+=d$ （未知该边是否为相等边=>若非相等边则依旧非相等便，若为相等边，则会被拉出相等子图，既然 $vy[i]=1$，则本次增广必然不会用到这条边，拉出去也无所谓，况且通过 $u$ 去找匹配的 $v$ 也不方便。因此不必而且不便于体现在程序中。而初学者也不必深究，不处理即可）
4. $vx[u]=1,vy[v]=0$ ，则 $slack[v]-=d$ （该边非相等边=>修改后可能为相等边=>可能提供新増广路。很重要，这是扩大相等子图的原理）

复杂度

km+dfs

• 每次扩大相等子图最少只能加入一条相等边，也就是最多会进行 $n^2$ 次扩大相等子图
• 每次扩大相等子图后都需要 dfs 增广，单次复杂度可达 $n^2$

也就是说，km+dfs 的复杂度可达 $n^4$

---

考虑如何优化，不难发现每次扩大相等子图后，都要从增广点重新开始 dfs ，这是非常浪费时间的

那么，能不能在扩大子图后，保留上次的状态呢

答案是可行的，我们只需要换 bfs 的写法：在每次扩大子图后，都记录一下新加入的相等边所为我们提供的新增广方向，然后从此处继续寻找增广路即可

km + bfs

扩大子图复杂度：

• 每次扩大相等子图至少只能加入一条相等边，也就是最多会进行 $n^2$ 次扩大相等子图
• 每次扩大相等子图复杂度 $n$（扫描加进相等子图的那个点的边），无需额外增广，从上次起点继续增广即可

增广复杂度

• 每个左部点需要 $1$ 次增广，共有 $n$ 个左部点
• 单次增广复杂度可达 $n^2$

km + bfs 的复杂度降到了 $n^3$

代码实现

km+DFS 实现

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF=1e9+7;
struct KM{
    int n;
    vector<vector<int> > E;
    vector<int> lx,ly,py,vx,vy;
    int d;

    void init(int n){
        this->n=n;
        E.resize(n+1);
        for(auto& e:E) e.assign(n+1,-INF);
        lx.assign(n+1,-INF);ly.assign(n+1,0);py.assign(n+1,0);
        vx.assign(n+1,0);vy.assign(n+1,0);
    }

    bool DFS(int u){
        vx[u]=1;
        for(int i=1;i<=n;i++)if(!vy[i]){
            if(lx[u]+ly[i]==E[u][i]){ //在相等子图中
                vy[i]=1;
                if(!py[i]||DFS(py[i])){
                    py[i]=u;vy[i]=1;
                    return 1;
                }
            }
            else d=min(d,lx[u]+ly[i]-E[u][i]);
        }
        return 0;
    }

    void km(){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++)
                lx[i]=max(lx[i],E[i][j]);
        }
        for(int i=1;i<=n;i++){
            while(true){
                d=INF;vx.assign(n+1,0);vy.assign(n+1,0);
                if(DFS(i))break;  //如果能匹配就不缩小子图
                for(int j=1;j<=n;j++){
                    if(vx[j])lx[j]-=d;
                    if(vy[j])ly[j]+=d;
                }
            }
        }
    }
};
int main(){
    freopen("P6577.in","r",stdin);
    int n,m;
    scanf("%d%d",&n,&m);
    KM F;F.init(n);
    for(int i=1;i<=m;i++){
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        F.E[x][y]=z;
    }
    F.km();
    LL ans=0;
    for(int i=1;i<=n;i++)
        ans=ans+F.E[F.py[i]][i];
    printf("%lld\n",ans);
    for(int i=1;i<=n;i++)
        printf("%d ",F.py[i]);
    return 0;
}

KM+BFS 实现

struct KM_BFS{
    int n;
    vector<vector<int> > E;
    vector<int> lx,ly,slack,py,px,pre;
    vector<bool> vx,vy;

    void init(int n){
        this->n=n;
        E.resize(n+1);
        for(auto& e:E) e.assign(n+1,-INF);
        lx.assign(n+1,-INF);ly.assign(n+1,0);
        px.assign(n+1,0);py.assign(n+1,0);
    }

    void aug(int v){  //回去找匹配，模拟DFS回溯
        int t;
        while(v){
            t=px[pre[v]];
            px[pre[v]]=v;
            py[v]=pre[v];
            v=t;
        }
    }

    void BFS(int st){
        pre.assign(n+1,0);slack.assign(n+1,INF);
        vx.assign(n+1,0);vy.assign(n+1,0);
        queue<int> Q;
        Q.push(st);
        while(1){
            while(!Q.empty()){
                int u=Q.front();Q.pop();
                vx[u]=1;
                for(int i=1;i<=n;i++) if(!vy[i]){
                    if(lx[u]+ly[i]-E[u][i]<slack[i]){
                        slack[i]=lx[u]+ly[i]-E[u][i];
                        pre[i]=u; //记录 u 的父节点是什么，方便回溯的时候匹配
                        if(slack[i]==0){  //在相等子图内
                            vy[i]=1;
                            if(!py[i]){aug(i);return ;} //有空的没匹配，那就匹配
                            else Q.push(py[i]); //把 i 的匹配的那个放到队列中，看能不能匹配上
                        }
                    }
                }
            }
            int d=INF;
            for(int i=1;i<=n;i++) 
                if(!vy[i]) d=min(d,slack[i]);
            for(int i=1;i<=n;i++){ //扩大子图
                if(vx[i]) lx[i]-=d;
                if(vy[i]) ly[i]+=d;else slack[i]-=d;
            }
            for(int i=1;i<=n;i++) if(!vy[i]){
                if(slack[i]==0){ //vy=0 且 slack[i]=0 表示新加进来的哪些 点
                    vy[i]=1;
                    if(!py[i]) {aug(i);return ;}//有空的没匹配，那就匹配
                    else Q.push(py[i]); //把 i 的匹配的那个放到队列中，看能不能匹配上
                }
            }
        }
    }

    void km(){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++)
                lx[i]=max(lx[i],E[i][j]);
        }

        for(int i=1;i<=n;i++){
            BFS(i);
        }
    }
};
signed main(){
    freopen("P6577.in","r",stdin);
    int n,m;
    scanf("%lld%lld",&n,&m);
    KM_BFS F;F.init(n);
    for(int i=1;i<=m;i++){
        int x,y,z;
        scanf("%lld%lld%lld",&x,&y,&z);
        F.E[x][y]=z;
    }
    F.km();
    LL ans=0;
    for(int i=1;i<=n;i++)
        ans=ans+F.E[F.py[i]][i];
    printf("%lld\n",ans);
    for(int i=1;i<=n;i++)
        printf("%lld ",F.py[i]);
    return 0;
}

转化为费用流

在图中新增一个源点和一个汇点。

从源点向二分图的每个左部点连一条流量为 $1$，费用为 0 的边，从二分图的每个右部点向汇点连一条流量为 $1$，费用为 $0$ 的边。

接下来对于二分图中每一条连接左部点 $u$ 和右部点 $v$，边权为 $w$ 的边，则连一条从 $u$ 到 $v$，流量为 $1$，费用为 $w$ 的边。

求这个网络的 最大费用最大流 即可得到答案。

二分图最小点覆盖（König 定理）

最小点覆盖：选最少的点，满足每条边至少有一个端点被选。

二分图中，最小点覆盖 $=$ 最大匹配。

证明

将二分图点集分成左右两个集合，使得所有边的两个端点都不在一个集合。

考虑一种构造最小点覆盖：从左侧未匹配的节点出发，按照匈牙利算法中增广路的方式走，即先走一条未匹配边，再走一条匹配边。由于已经求出了最大匹配，所以这样的「增广路」一定以匹配边结束，即增广路是不完整的。（如果以非匹配边结束，则会出现一条完整的增广路）在所有经过这样「增广路」的节点上打标记

如图就是一个二分图，红色为匹配边，黑色为非匹配边

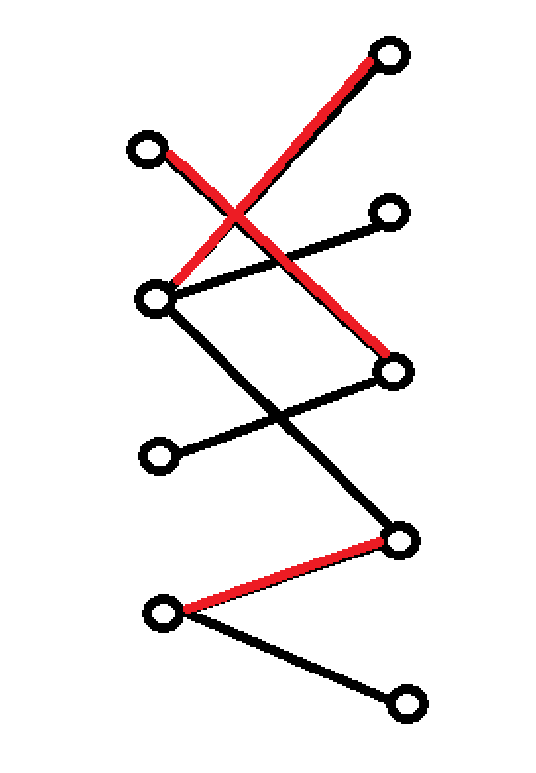
打上标记的就是圈内变蓝的点。

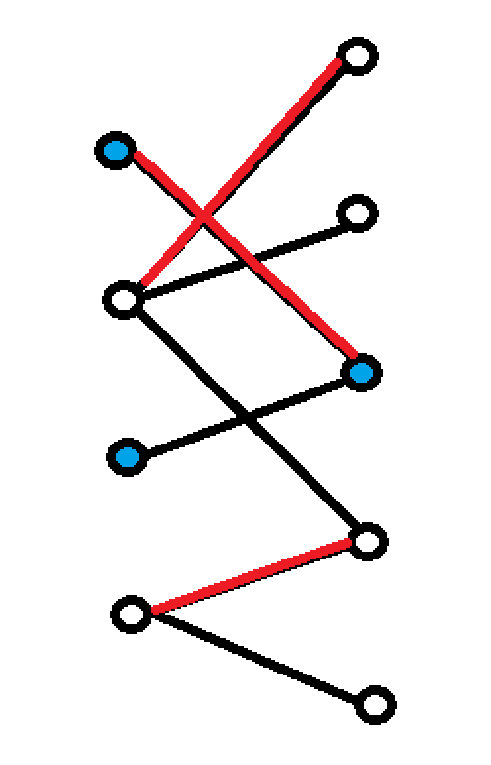
则最后构造的集合是：所有左侧未打标记的节点和所有右侧打了标记的节点，也就是绿圈起来的点

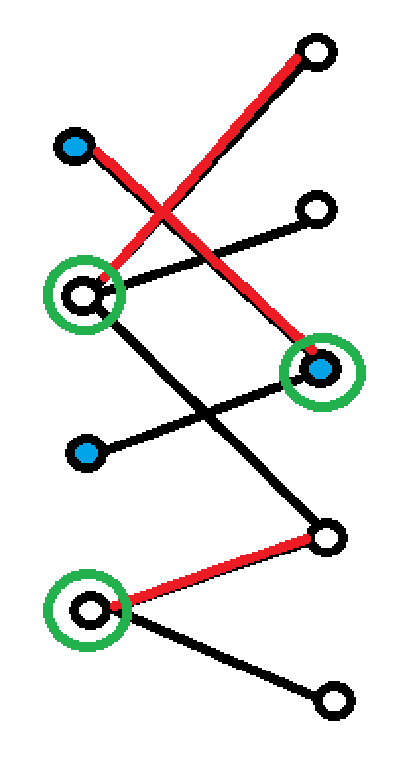
一、这个集合的大小等于最大匹配。

• 每个集合中的点对应一条匹配边：
  • 左边未打标记的点都一定对应着一个匹配边（否则会以这个点为起点开始标记）
  • 右边打了标记的节点一定在一条不完整的增广路上，也会对应一个匹配边。
• 每条匹配边都对应一个集合中的点
  • 假设存在一条匹配边左侧标记了，右侧没标记，左边的点只能是通过另一条匹配边走过来，此时左边的点有两条匹配边，不符合最大匹配的规定；
  • 假设存在一条匹配边左侧没标记，右侧标记了，那就会从右边的点沿着这条匹配边走过来，从而左侧也有标记。

因此，每一条匹配的边两侧一定都有标记（在不完整的增广路上）或都没有标记，这也代表着：匹配边的两个节点中必然只有一个被选中。所以选中集合大小=匹配边条数

二、这个集合是一个点覆盖。由于我们的构造方式是：所有左侧未打标记的节点和所有右侧打了标记的节点。

假设存在左侧打标记且右侧没打标记的边

• 对于匹配边，上一段已经说明其不存在
• 对于非匹配边，右端点一定会由这条非匹配边经过，从而被打上标记。

因此，这样的构造能够覆盖所有边。

同时，不存在更小的点覆盖。为了覆盖最大匹配的所有边，至少要有最大匹配边数的点数。

二分图最大独立集

最大独立集：选最多的点，满足两两之间没有边相连。

因为在最小点覆盖中，任意一条边都被至少选了一个顶点，所以对于其点集的补集，任意一条边都被至多选了一个顶点，所以不存在边连接两个点集中的点，且该点集最大。因此二分图中，最大独立集 $=n-$最小点覆盖