引入

来看一道例题 洛谷 P2495 [SDOI2011] 消耗战 (opens new window)

显然，最朴素的办法是对于每次询问都进行一次树形dp，我们称含有资源的点为关键节点

定义 $dp[u]$ 表示 $u$ 和子树中所有关键点都不链接的最小花费

枚举到 $u$ 时，遍历子节点 $v$

• 若 $v$ 是关键节点，那么久需要断开 $u-v$ 这条边，所以 $dp[u]+=w$
• 若 $v$ 不是关键节点，可以考虑断或者不断 $dp[u]+=\min(w,dp[v])$

显然，答案是 $dp[1]$，时间复杂度为 $O(nm)$ 会 TLE，考虑优化

实现

我们观察到 $\sum k=5\times 10^5$，表示其实树中有很多无用节点，只需要关注关键节点，以及关键点的 LCA 即可

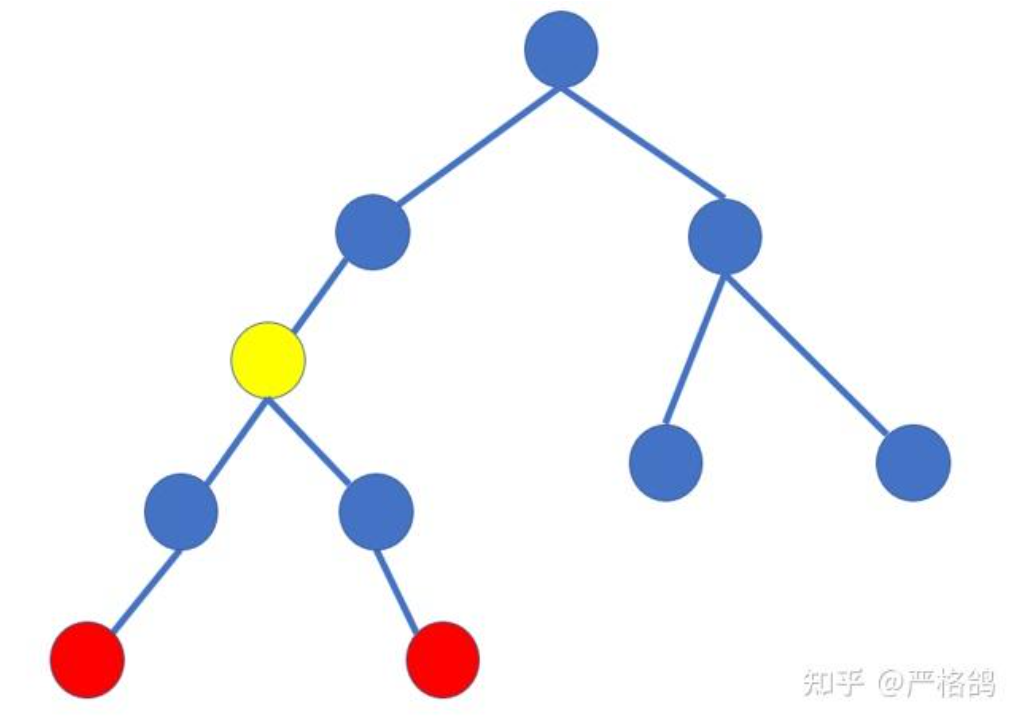
发现，对于这样的边，我们可以只保留其路径中的最小值即可

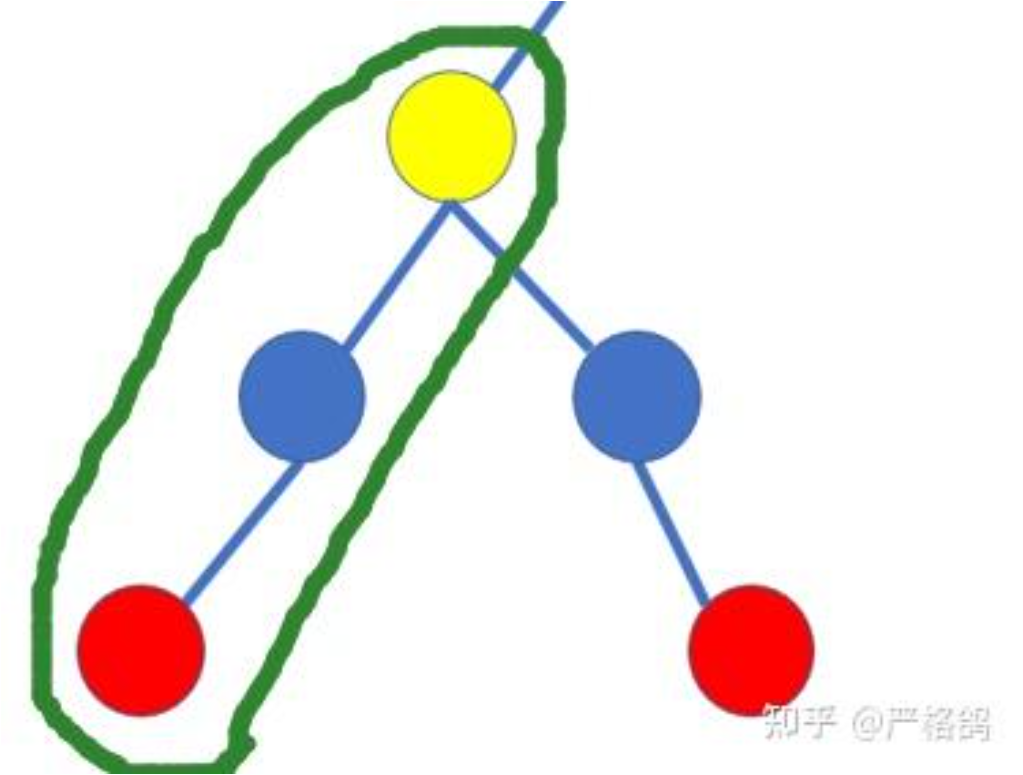
于是，我们可以把整棵树缩小

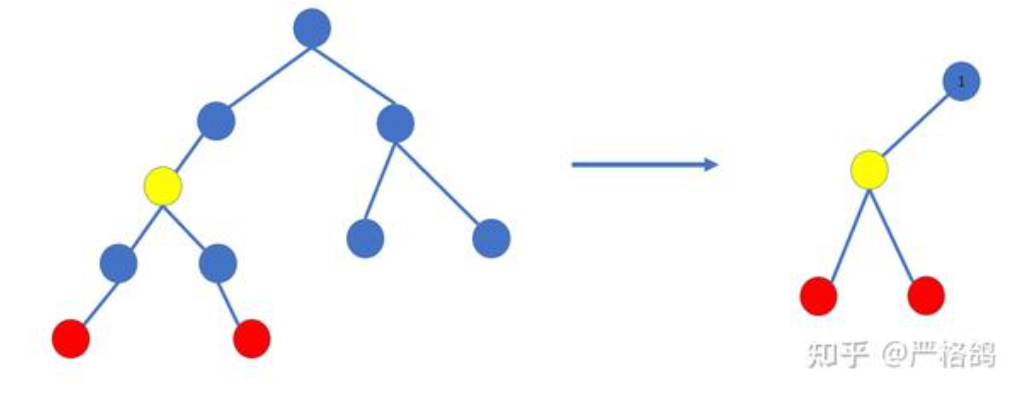
对于这个题目的特殊性，我们可以用从 $1$ 到 $u$ 的路径的最小值，来表示 $u$ 链接其父节点的边，因为只需要和 $1$ 号点断开即可

我们称，这样的新的树为虚树

如何建树，我们使用单调栈来建树，就是用一个栈模拟 dfs 的过程

需要定义一个函数 isp(u, v) 来判断 $v$ 是否是 $u$ 的子树

int isp(int u, int v) {
    return in[u] <= in[v] && out[v] <= out[u];
}

由于，在使用栈模拟的过程中可能出现把栈弹空仍不能出现其 $LCA$，所以需要把 LCA 提前塞入数组中

我们先对于关键点 node 的 dfs 序进行排序，然后对相邻节点计算 LCA，把 LCA 塞进 node，去重后，再使用栈模拟

• 如果 $v$ 是 $u$ 的儿子，就建立 $u-v$ 这条边
• 如果 $v$ 不是 $u$ 的儿子，就把 $u$ 弹出，直到找到 $u'$ 使得 $v$ 是 $u'$ 的儿子

然后在新建的树上跑之前的那个 dp 即可

void build(vector<int>&node) {
    sort(node.begin(), node.end(), cmp);
    set<int>node_st; for (int x : node)node_st.insert(x);
    for (int i = 1; i < node.size(); i++)node_st.insert(lca(node[i - 1], node[i]));
    node.clear();for (int x : node_st)node.push_back(x);
    sort(node.begin(), node.end(), cmp);
    vector<int> st;
    for (int v : node) {
        while (!st.empty() && !isp(st.back(), v))
            st.pop_back();
        if (!st.empty())
            vg[st.back()].push_back({ v ,mi[v] });
        st.push_back(v);
    }
}

在实际写代码时要注意 node 可能达到题目给出的两倍

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int MAXN = 1e6 + 5;
int n, q;
vector<pair<int, int>> g[MAXN];

int mi[MAXN], in[MAXN], out[MAXN];
int dfn = 0;
void init(int u, int fa) {
    in[u] = ++dfn;
    for (auto [v, w] : g[u]) {
        if (v == fa) continue;
        mi[v] = min(mi[u], w);
        init(v, u);
    }
    out[u] = dfn;
}

int f[MAXN][21], dep[MAXN];
void dfs_lca(int u, int fa) {
    f[u][0] = fa; dep[u] = dep[fa] + 1;
    for (int i = 1; i <= 20; i++)
        f[u][i] = f[f[u][i - 1]][i - 1];
    for (auto [v, w] : g[u]) {
        if (v == fa) continue;
        dfs_lca(v, u);
    }
}

int lca(int u, int v) {
    if (dep[u] < dep[v]) swap(u, v);
    for (int i = 20; i >= 0; i--)
        if (dep[f[u][i]] >= dep[v]) u = f[u][i];
    if (u == v) return u;
    for (int i = 20; i >= 0; i--)
        if (f[u][i] != f[v][i]) u = f[u][i], v = f[v][i];
    return f[u][0];
}

int isp(int u, int v) {
    return in[u] <= in[v] && out[u] >= out[v];
}

bool cmp(int u, int v) {
    return in[u] < in[v];
}

int vis[MAXN];
vector<pair<int,int>> vg[MAXN];

void build(vector<int> &node) {
    sort(node.begin(), node.end(), cmp);
    set<int> st; for (int x : node) st.insert(x);
    for (int i = 1; i < (int)node.size(); i++) st.insert(lca(node[i - 1], node[i]));
    node.clear(); for (int x : st) node.push_back(x);
    sort(node.begin(), node.end(), cmp);
    stack<int> stk;
    for (int v : node) {
        while (!stk.empty() && !isp(stk.top(), v)) stk.pop();
        if (!stk.empty()) vg[stk.top()].push_back({v, mi[v]});
        stk.push(v);
    }
}

int dp[MAXN];
void dfs_dp (int u) {
    dp[u] = 0;
    for (auto [v, w] : vg[u]) {
        dfs_dp(v);
        if (vis[v]) dp[u] += w;
        else dp[u] += min(dp[v], w);
    }
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cin >> n;
    for (int i = 1; i < n; i++) {
        int u, v, w; cin >> u >> v >> w;
        g[u].push_back({v, w});
        g[v].push_back({u, w});
    }
    memset(mi, 0x3f, sizeof mi);
    init(1, 0);
    dfs_lca(1, 0);
    int q; cin >> q;
    while (q--) {
        int k; cin >> k;
        vector<int> node(k);
        for (int i = 0; i < k; i++) 
            cin >> node[i], vis[node[i]] = 1;
        node.push_back(1);
        build(node);
        dfs_dp(1);
        cout << dp[1] << endl;
        for (int x : node) vg[x].clear(), vis[x] = 0;
    }
    return 0;
}