AtCoder Beginner Contest 347 (opens new window)

A - Divisible

Quesiton

给你正整数 $N$ 和 $K$ ，以及长度为 $N$ 的序列 $A$。

提取 $A$ 中所有是 $K$ 倍数的元素，除以 $K$ ，并打印商。

Solution

判断 $A_i \% K$ 的值是否为 $0$，如果非 $0$ 则表示可以整除

Code

#include <bits/stdc++.h>
using namespace std;
int main() {
    vector<int> ans;
    int n, k; cin >> n >> k;
    for (int i = 1; i <= n;i++) {
        int x; cin >> x;
        if (x % k == 0) {
            ans.push_back(x / k);
        }
    }
    for (auto x : ans)
        cout << x << " ";
    return 0;
}

B - Substring

Question

给你一个由小写英文字母组成的字符串 $S$ 。 $S$ 有多少个不同的非空子串？

子串是连续的子序列。例如，xxx是yxxxy的子串，但不是xxyxx的子串。

Solution

使用 substr() 函数取字串

然后用 set<string> 去重即可

Code

#include <bits/stdc++.h>
using namespace std;
int main() {
    string s; cin >> s;
    set<string> st;
    for (int L = 1; L <= s.size(); L++) 
        for (int i = 0; i + L - 1 < s.size(); i++) {
            string t = s.substr(i, L);
            st.insert(t);
        }
    cout << st.size() << endl;
    return 0;
}

C - Ideal Holidays

Soluiton

考虑把一个 $D_i$ 都压缩到一个周期中

$D_i = (D_i-1)\%(A+B)$

即 $0$ 表示一周的第一天，$A+B-1$ 表示一周的最后一天

我们需要找一个 $i$ 使得 $[i,i+A)$ 天包括所有的 $D_i$

如果 $i+A>A+B$ ，即 $i>B$，那么就可以转化成：

$[0,i-B)\cup[i,n)$

具体实现是，转化为判断

排序后，是否存在一个 $D_i$ 和 $D_{i+1}$ 的中间能插入一个 $B$

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
    int n; cin >> n;
    ll A, B; cin >> A >> B;
    vector<ll> D(n);
    for (int i = 0; i < n; i++) {
        cin >> D[i];
        D[i] = (D[i] - 1) % (A + B);
    }
    sort(D.begin(), D.end());
    for (int i = 1; i < n; i++)
        if (D[i] - D[i - 1] >= B) {
            cout << "Yes" << '\n';
            return 0;
        }
    if (D.back() - D.front() < A) {
        cout <<  "Yes" << '\n';
        return 0;
    }
    cout << "No" << endl;
    return 0;
}

D - Popcount and XOR

Solution

由于异或的性质，每一位分开来看，如果为 $1$，说明两者肯定有一个为 $0$，一个为 $1$，如果为 $0$，有可能都为 $0$，或都为 $1$

我们设 $C$ 的二进制位数 $1$ 的个数为 $cnt_c$

所以 $a+b<cnt_c$ 或者 $a+b-cnt_c$ 是一个奇数的情况肯定是不合法的

然后模拟放 $1$ 的过程

如果 $C$ 的某一位为 $1$，选择 $a$ 或 $b$ 其中的一个放 $1$

在 $C$ $1$ 的位置都放完后，如果 $a,b$ 还有剩余，就在 $C$ 为 $0$ 的位置同时在 $a,b$ 的相同位置放上 $1$

使用 bitset 可以很好的模拟

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
    int a, b;
    ll C; 
    cin >> a >> b >> C;
    bitset<60> bit_C(C), bit_A, bit_B;
    if (a + b < bit_C.count() || (a + b - bit_C.count()) % 2 == 1) {cout << "-1" << '\n'; return 0;}
    int cnt = (a + b - bit_C.count()) / 2;
    a -= cnt; b -= cnt;
    for (int i = 0; i < 60; i++) {
        if (bit_C[i]) {
            if (a) {bit_A[i] = 1; a--;}
            else if (b) {bit_B[i] = 1; b--;}
        }
    }
    if (a != 0 || b != 0) {cout << "-1" << '\n'; return 0;}
    for (int i = 0; i < 60; i++) 
        if (bit_C[i] == 0)
            if (cnt) {
                bit_A[i] = 1; bit_B[i] = 1; cnt--;
            }
    if (cnt) {cout << "-1" << '\n'; return 0;}
    cout << bit_A.to_ullong() << ' ' << bit_B.to_ullong() << '\n';
    return 0;
}

E - Set Add Query

Solution

提前用 set<int> 模拟出第 $i$ 个询问后的 $S$ 的大小，设为 $siz[i]$

对于每个数，答案就是，奇数次出现 $\sim$ 偶数次出现的 $siz$ 的和

直接用树状数组或前缀和就可以快速得到

如果最后一个是奇数次，那么就加上个点到最后所有的 $siz$

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
    freopen ("E.in","r",stdin);
    int n, Q; cin >> n >> Q;
    vector<int> q(Q + 1, 0);
    for (int i = 1; i <= Q; i ++)
        cin >> q[i];
    set<int> st;
    vector<ll> cnt(Q + 1, 0);
    for (int i = 1; i <= Q; i++) {
        int x = q[i];
        if (st.count(x)) 
            st.erase(x);
        else
            st.insert(x);
        cnt[i] = st.size();
    }
    
    vector<vector<int> > pos(n + 1, vector<int>());
    for (int i = 1; i <= Q; i++)
        pos[q[i]].push_back(i);
    
    vector<ll> c(Q + 1, 0);
    auto add = [&](int x, int v) {
        for (; x <= Q; x += x & -x)
            c[x] += v;
    };
    auto query = [&](int x) {
        ll res = 0;
        for (; x; x -= x & -x)
            res += c[x];
        return res;
    };

    for (int i = 1; i <= Q; i++) 
        add(i, cnt[i]);
    
    for (int i = 1; i <= n; i++) {
        ll ans = 0;
        if (pos[i].size() & 1)
            pos[i].push_back(Q + 1);
        
        for (int j = 0; j < pos[i].size(); j += 2) {
            ans += query(pos[i][j + 1] - 1) - query(pos[i][j] - 1);
        }
        cout << ans << ' ';
    }
    return 0;
}

F - Non-overlapping Squares

Solution

先考虑两个 $M\times M$ 正方形的情况

显然，存在一条线，把 $N\times N$ 的正方形切成两个矩形，$M\times M$ 的正方形分别在一个矩形中

所以推广到三个 $M\times M$ 的正方形，就会出现 $6$ 种情况：

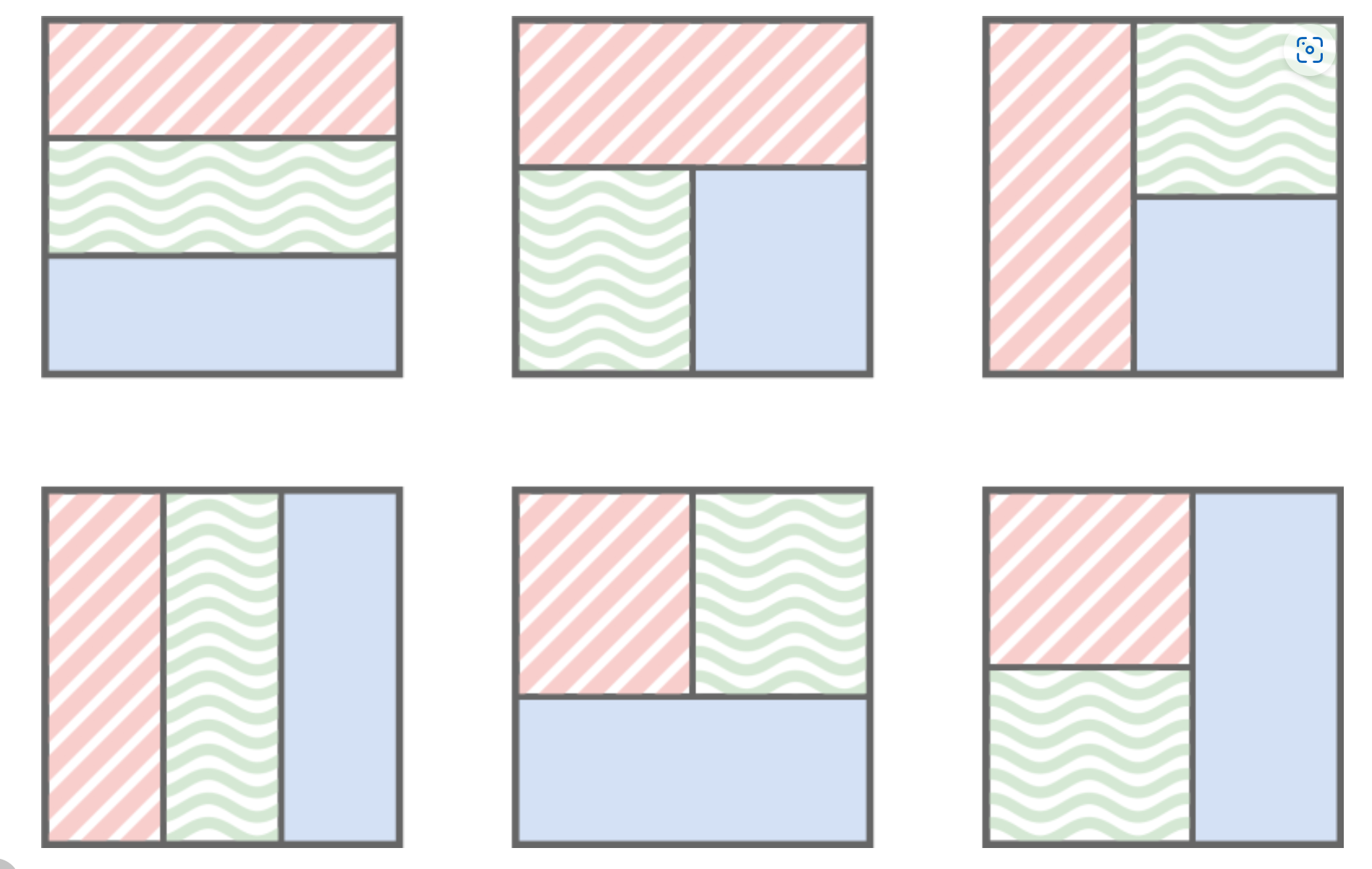
每个 $M\times M$ 的正方形必然分别在一个矩形中

我们先求出每个点为右下角作的点的 $M\times M$ 的区间和

然后对于每个单独的矩形块，只需要找矩形内的最大值即可

可以使用线段树套线段树解决，时间复杂度为 $O(n^2\log ^2 n)$

我在具体实现时只写了三个，然后通过旋图去求另外三个

Code

#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll inf = 1e17;
const int maxn = 1e3 + 1;

ll maxv[maxn << 2][maxn << 2];

struct Segment_Tree {
    int n;

    void build_y (int u, int rt, int l, int r) {
        maxv[rt][u] = -inf;
        if (l == r) return;
        int mid = (l + r) >> 1;
        build_y(u << 1, rt, l, mid);
        build_y(u << 1 | 1, rt, mid + 1, r);
    }

    void build_x (int u, int l, int r) {
        build_y (1, u, 1, n);
        if (l == r) return;
        int mid = (l + r) >> 1;
        build_x(u << 1, l, mid);
        build_x(u << 1 | 1, mid + 1, r);
    }

    void init(int _n) {
        n = _n;
        build_x(1, 1, n);
    }

    void update_y(int u, int rt, int l, int r, int y, ll val) {
        if (l == r) {
            maxv[rt][u] = max(maxv[rt][u], val);
            return;
        }
        int mid = (l + r) >> 1;
        if (y <= mid) update_y(u << 1, rt, l, mid, y, val);
        else update_y(u << 1 | 1, rt, mid + 1, r, y, val);
        maxv[rt][u] = max(maxv[rt][u << 1], maxv[rt][u << 1 | 1]);
    }
    void update_x(int u, int l, int r, int x, int y, ll val) {
        update_y(1, u, 1, n, y, val);
        if (l == r) return;
        int mid = (l + r) >> 1;
        if (x <= mid) update_x(u << 1, l, mid, x, y, val);
        else update_x(u << 1 | 1, mid + 1, r, x, y, val);
    }
    ll query_y (int u, int rt, int l, int r, int ql, int qr) {
        if (ql <= l && r <= qr)
            return maxv[rt][u];
        int mid = (l + r) >> 1;
        ll res = -inf;
        if (ql <= mid)
            res = max(res, query_y(u << 1, rt, l, mid, ql, qr));
        if (qr > mid)
            res = max(res, query_y(u << 1 | 1, rt, mid + 1, r, ql, qr));
        return res;
    }
    ll query_x (int u, int l, int r, int qlx, int qrx, int qly, int qry) {
        if (qlx <= l && r <= qrx)
            return query_y (1, u, 1, n, qly, qry);
        int mid = (l + r) >> 1;
        ll res = -inf;
        if (qlx <= mid)
            res = max(res, query_x(u << 1, l, mid, qlx, qrx, qly, qry));
        if (qrx > mid)
            res = max(res, query_x(u << 1 | 1, mid + 1, r, qlx, qrx, qly, qry));
        return res;
    }
}st;

ll sum[maxn][maxn], a[maxn][maxn];

ll solve (int n, int m, vector<vector<ll> >& mp) {
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + mp[i][j]; // 2维前缀和
        
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++) {
            if (i < m || j < m) { a[i][j] = -inf; continue; }
            a[i][j] = sum[i][j] - sum[i - m][j] - sum[i][j - m] + sum[i - m][j - m]; // 2维区间和
        }
    
    st.init(n);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            st.update_x(1, 1, n, i, j, a[i][j]);
    
    ll ans = -inf, now_1, now_2, now_3;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++) {
            if (i >= m && j - i >= m && n - j >= m) {
                now_1 = st.query_x (1, 1, n, 1, n, 1, i);
                now_2 = st.query_x (1, 1, n, 1, n, i + m, j);
                now_3 = st.query_x (1, 1, n, 1, n, j + m, n);
                ans = max(ans, now_1 + now_2 + now_3);
            }

            if (i >= m && j >= m && n - j >= m && n - i >= m) {
                now_1 = st.query_x (1, 1, n, 1, i, 1, n);
                now_2 = st.query_x (1, 1, n, i + m, n, 1, j);
                now_3 = st.query_x (1, 1, n, i + m, n, j + m, n);
                ans = max(ans, now_1 + now_2 + now_3);
            }

            if (i >= m && n - i >= m && j >= m && n - j >= m) {
                now_1 = st.query_x (1, 1, n, i + m, n, 1, n);
                now_2 = st.query_x (1, 1, n, 1, i, 1, j);
                now_3 = st.query_x (1, 1, n, 1, i, j + m, n);
                ans = max(ans, now_1 + now_2 + now_3);
            }
        }
    return ans;
}

inline ll read_ll() {
    ll x = 0, f = 1; char ch = getchar();
    while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
    while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
    return x * f;
}

inline int read_int() {
    int x = 0, f = 1; char ch = getchar();
    while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
    while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
    return x * f;
}

int main() {
    freopen ("F.in", "r", stdin);
    freopen ("F.out", "w", stdout);
    int n, m; n = read_int(); m = read_int();
    vector<vector<ll> > mp(n + 1, vector<ll>(n + 1, 0)), sum(n + 1, vector<ll>(n + 1, 0));
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            mp[i][j] = read_ll();
    
    ll ans = solve(n, m, mp);
    for (int k = 0; k < 1; k++) {
        // rotate 90 degree
        vector<vector<ll> > tmp(n + 1, vector<ll>(n + 1, 0));
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                tmp[i][j] = mp[j][n - i + 1];
        mp = tmp;
        ans = max(ans, solve(n, m, mp));
    }
    cout << ans << endl;
    return 0;
}

G - Grid Coloring 2

Solution

非常有意思一个题

我们利用拆点的思想，把问题转化成一个网络流模型

把一个点拆成 4 个点 $1,2,3,4$

然后建立一个超级原点 $S$ 和一个超级汇点 $T$

考虑这样建边：

(1) 对于每个点 $(x,y)$

建边 $(x,y)_{k+1} \rightarrow (x,y)_{k}(1\le k < 4)$

这保证了， $T\rightarrow$ $B_{x,y}$ 的完整性

(2) 对于一个点 $A_{x,y} = p$，

如果 $p>1$ 建边 $S\rightarrow (x,y)_{p-1}$，

如果 $p<5$ 建边 $(x,y)_{p}\rightarrow T$

这保证了，$(x,y)$ 只能在 $A_{x,y}$ 处分断

(3) 对于与 $(x,y)$ 相邻的点 $(x',y')$

建边 $(x,y)_{k}\rightarrow (x',y')_{k}$ ，边权为 $1$

建边 $(x,y)_k\rightarrow (x',y')_v\ (1\le v < k)$ ，边权为 $2$

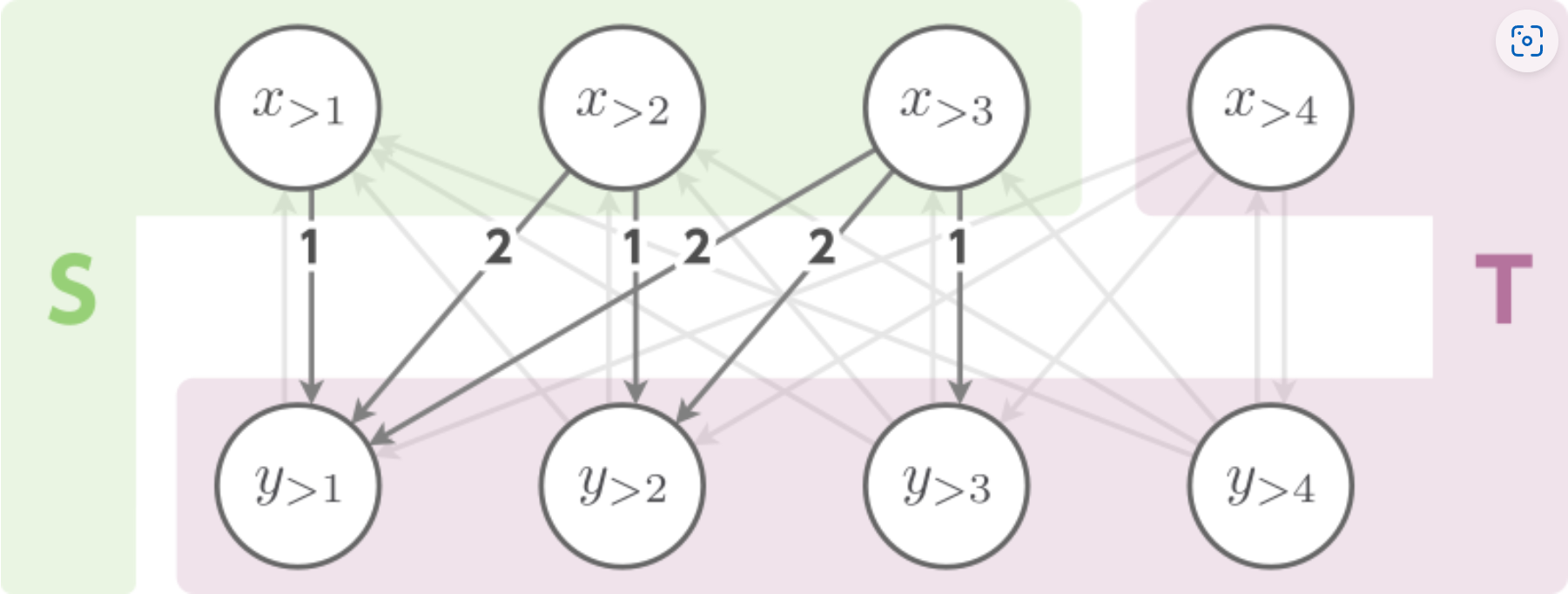
这里用到了一个很妙的性质，$1+3+\cdots+(2k+1)=k^2$

此时 $B_x = 4,B_y=1$

则所需要的代价就是 $1+(2+1)+(2+2+1)=9$

如果 $B_x,B_y$ 相差 $k$，那么就按照上面的公式这样累加，来实现平方数

则 $S-T$ 最小割就是答案

Code

#include <bits/stdc++.h>
#include <atcoder/maxflow>
using namespace std;

const int inf = 0x3f3f3f3f;

int main() {
    int n; cin >> n;
    atcoder::mf_graph<int> g(1 + 4 * n * n + 1);
    const int S = 0, T = 1 + 4 * n * n;
    const auto id = [&] (int x, int y, int v) {
        return (x * n + y) * 4 + v;
    };
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            for (int v = 1; v + 1 <= 4; v++) 
                g.add_edge(id(i, j, v + 1), id(i, j, v), inf);
    
    for (int i = 0; i < n; i++)
        for (int j = 0; j + 1 < n; j++)
            for (int v = 1; v <= 4; v++) {
                g.add_edge(id(i, j, v), id(i, j + 1, v), 1);
                g.add_edge(id(i, j + 1, v), id(i, j, v), 1);
                for (int u = 1; u < v; u++) {
                    g.add_edge(id(i, j, v), id(i, j + 1, u), 2);
                    g.add_edge(id(i, j + 1, v), id(i, j, u), 2);
                }
            }
    
    for (int i = 0; i + 1 < n; i++)
        for (int j = 0; j < n; j++)
            for (int v = 1; v <= 4; v++) {
                g.add_edge(id(i, j, v), id(i + 1, j, v), 1);
                g.add_edge(id(i + 1, j, v), id(i, j, v), 1);
                for (int u = 1; u < v; u++) {
                    g.add_edge(id(i, j, v), id(i + 1, j, u), 2);
                    g.add_edge(id(i + 1, j, v), id(i, j, u), 2);
                }
            }

    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++) {
            int x; cin >> x;
            if (x == 0) continue;
            if (x < 5)
                g.add_edge(id(i, j, x), T, inf);
            if (x > 1) 
                g.add_edge(S, id(i, j, x - 1), inf);
        }
    
    g.flow(S, T);
    const auto &cut = g.min_cut(S);
    
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            int x = 1;
            for (int v = 1; v <= 4; v++)
                x += cut[id(i, j, v)];
            cout << x << ' ';
        }
        cout << '\n';
    }
    return 0;
}