 凸包
凸包
# 凸包
# 定义
凸包就是把定点包在内部的,面积最小的凸多边形。
首先把所有点按照 从大到小排序(如果 相同,则按照 从大到小排序)删除重复点后得到序列
# Andrew 算法求凸包
显然,排序后最小的元素和最大的元素一定在凸包上,且从左向右看,上下凸壳的旋转方向不同,所以我们先升序枚举求出下凸壳,然后降序求出上凸壳
然后把 放到凸包中,从 开始,当新点在图片“前进”方向的左边时继续,否则一次删除最近加入凸包的点,直到新点在凸包左边
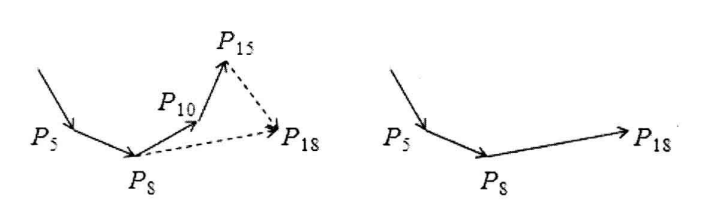
这个算法时间复杂度时 ,加上排序后的时间复杂度为
vector<Point> convexhull(vector<Point> p) {
int n = p.size();
sort(p.begin(), p.end(), [](Point a, Point b) {
return a.x < b.x || (a.x == b.x && a.y < b.y);
});
vector<int> ch(n * 2); int m = 0;
for (int i = 0; i < n; i++) {
while (m > 1 && cross(p[ch[m - 1]] - p[ch[m - 2]], p[i] - p[ch[m - 2]]) <= 0) m--;
ch[m++] = i;
}
for (int i = n - 2, t = m; i >= 0; i--) {
while (m > t && cross(p[ch[m - 1]] - p[ch[m - 2]], p[i] - p[ch[m - 2]]) <= 0) m--;
ch[m++] = i;
}
if (n > 1) m--;
// 这里的 p 为重新排序过了,如果返回 ch 数组想得到按顺序的值需要把原序列重新排序或者把 p 改成引用
vector<Point> res(m);
for (int i = 0; i < m; i++) res[i] = p[ch[i]];
return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
上次更新: 2025/04/08, 18:03:31
