AtCoder Beginner Contest 359 (opens new window)

A - Count Takahashi

Code

#include <bits/stdc++.h>
using namespace std;
int main() {
    int N; cin >> N;
    int cnt = 0;
    for (int i = 1; i <= N; i++) {
        string s; cin >> s;
        if (s == "Takahashi")
            cnt++;
    }
    cout << cnt << endl;
    return 0;
}

B - Couples

Code

#include <bits/stdc++.h>
using namespace std;
int main() {
    ios::sync_with_stdio(false);
    int N; cin >> N;
    vector<vector<int> > p(N,vector<int>());
    for (int i = 1; i <= 2 * N; i++) {
        int col; cin >> col;
        p[col-1].push_back(i);
    }
    int cnt = 0;
    for (auto v : p) {
        if (abs(v[0] - v[1]) == 2)
            cnt += 1;
    }
    cout << cnt << endl;
    return 0;
}

C - Tile Distance 2

Solution

算是比较恶心的一道 C 了

我们发现 $y$ 坐标之差说明了需要穿过横的线的次数，但是我 $x$ 坐标之差并不代表穿过竖的线的次数

因为每次可以通过纵向位移来达到横向位移

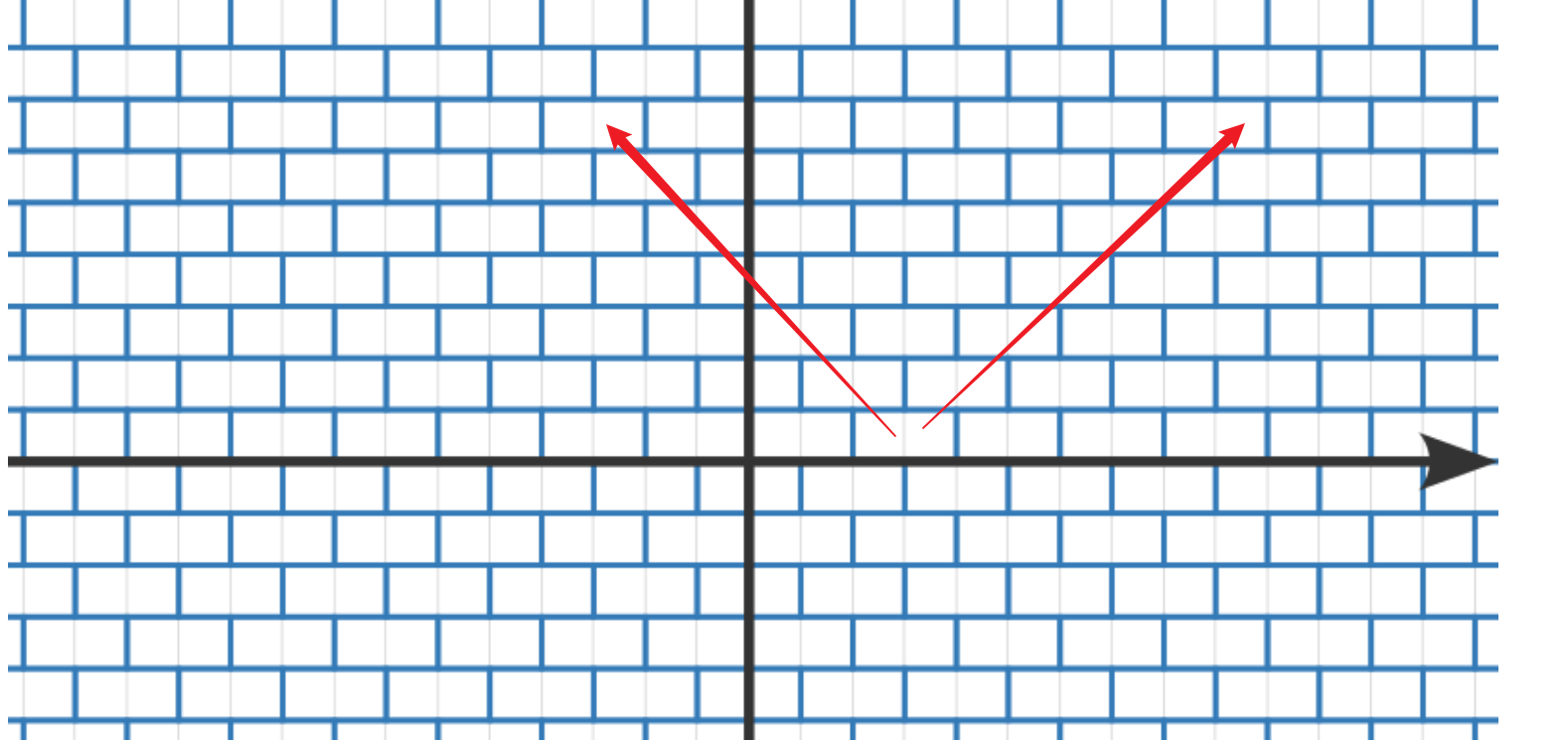
箭头的格点是不需要穿过竖着的线的

那么我们只需要算出箭头的范围，对于箭头外的点，穿过竖着的线的次数就是横坐标之差 / $2$

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int check (ll x, ll y) {
    if (x % 2 == 0 && y % 2 == 0) return 0;
    if (x % 2 == 1 && y % 2 == 1) return 0;
    return 1;
}

int main() {
    freopen ("C.in", "r", stdin);
    ios::sync_with_stdio(false);
    ll Sx, Sy, Tx, Ty; cin >> Sx >> Sy >> Tx >> Ty;
    if (Sx < Tx) { swap(Sx, Tx); swap(Sy, Ty); }
    ll dy = abs(Ty - Sy);
    ll pos_x = Sx - dy;
    if (check(Sx, Sy) == 1) pos_x -= 1;
    if (check(Tx, Ty) == 1) Tx -= 1;
    ll dx = max(0ll, (pos_x - Tx) / 2);
    cout << dx + dy << endl;
    return 0;
}

D - Avoid K Palindrome

Question

给定一个长度为 $N$ 的字符串 $S$，由字符 A 、 B 和 ? 组成。

同时给定正整数 $K$。如果一个由 A 和 B 组成的字符串$T$满足以下条件，则称其为好字符串：

• $T$ 中长度为 $K$ 的任意连续子串都不是回文串。

令 $q$ 为 $S$ 中 ? 的个数。将 $S$ 中的每个 ? 替换成 A 或 B ，可以得到 $2^q$ 个字符串。求这些字符串中有多少个是好字符串。

由于计数可能非常大，因此请对$998244353$取模。

Solution

发现 $N\le 10$ 很小，考虑把 $N$ 用二进制表示塞入 DP 里

用 $0$ 代表 $A$，用 $1$ 代表 $B$

定义 $F[i][s]$ 表示枚举到第 $i$ 位，前 $N-1$ 位用二进制表示是 $s$ 的好字符串个数

假设这一位的带选项为 $x=0/1$

如果 $(s << 1) |x$ 为回文的话就不能转移，否则考虑转移

$F[i+1][((s<<1|x)\%(N-1))\leftarrow F[i][s]$

Code

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int TT = 998244353;
signed main() {
    freopen ("D.in", "r", stdin);
    ios::sync_with_stdio(false);
    int N, K; cin >> N >> K;
    vector<int> huiwen(1 << K, 0);

    auto check = [&] (int x) {
        vector<int> cnt(K, 0);
        for (int i = 0; i < K; i++)
            if (x & (1 << i))
                cnt[i] = 1;
        for (int i = 0; i < K; i++)
            if (cnt[i] != cnt[K - i - 1])
                return 0;
        return 1;
    };

    for (int i = 0; i < (1 << K); i++)
        huiwen[i] = check(i);
    
    vector dp(N + 1, vector<int>(1 << K, 0));
    
    string s; cin >> s;
    vector<int> p;
    dp[0][0] = 1;
    for (int i = 0; i < N; i++) {
        p.clear();
        if (s[i] == 'A') p.push_back(0);
        if (s[i] == 'B') p.push_back(1);
        if (s[i] == '?') p.push_back(0), p.push_back(1);
        for (int j = 0; j < (1 << (K - 1)); j++) {
            for (auto _ : p) {
                if (i + 1 >= K && huiwen[(j << 1) | _] == 1)
                    continue;
                int nxt = ((j << 1) | _) % (1 << K - 1);
                dp[i + 1][nxt] = (dp[i + 1][nxt] + dp[i][j]) % TT;
            }
        }
    }
    int ans = 0;
    for (int i = 0; i < (1 << K - 1); i++)
        ans = (ans + dp[N][i]) % TT;
    cout << ans << endl;
    return 0;
}

E - Water Tank

Solution

想要水满到这个挡板，那么需要这个挡板 $i$ 已经在 $i$ 前面的挡板 $j$ ，$H_j > H_i, j <i$， $j\sim i$ 这一区域里面都注入了 $H_i$ 的水，然后通过 $ans_j$ 能算出 $ans_i$，即：

$ans_i=ans_j+H_i\times(i-j)$

显然，我们需要去寻找在我之前比我大的，用单调栈就可以实现

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll INF = 0x3f3f3f3f;
int main() {
    freopen ("E.in", "r", stdin);
    ios::sync_with_stdio(false);
    int n; cin >> n;
    vector<ll> H(n + 1); H[0] = INF;
    vector<ll> ans(n + 1, 0);
    stack<ll> stk; stk.push(0);
    for (int i = 1; i <= n; i++)
        cin >> H[i];
    for (int i = 1; i <= n; i++) {
        while (H[stk.top()] < H[i]) stk.pop();
            ans[i] = ans[stk.top()] + (i - stk.top()) * H[i];
        stk.push(i);
    }
    for (int i = 1; i <= n; i++)
        cout << ans[i] + 1 << " ";
    return 0;
}

F - Tree Degree Optimization

Solution

树的度有一些性质，比如 $\sum du[i]=2n-2$, $du[i] \ge 1$

显然我们把这个问题看成一个数学问题，而不是一个树上问题，考虑 $du$ 的分配

已知 $du$ 的和为 $2n-2$ 并且，$du$ 至少为 $1$ ，那么我们需要继续分配 $n-2$ 个

每次 $du[i]+1$ 总和就会增加 $((du[i]+1)^2-du[i]^2)A[i]=(2du[i]+1)A[i]$

所以贪心的思维，我们只需要每次去最小的 $(2du[i]+1)A[i]$ 然后把这个 $du[i]+1$ 即可

用优先队列或者堆能很好的完成这个过程

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll, int> pli;
ll calc(ll x) {
    return (x + 1) * (x + 1) - x * x;
}
int main() {
    freopen ("F.in", "r", stdin);
    ios::sync_with_stdio(false);
    int n; cin >> n;
    vector<ll> a(n + 1), d(n + 1, 0);
    priority_queue<pli, vector<pli>, greater<pli> > pq;
    for (int i = 1; i <= n; i++) {
        d[i] = 1;
        cin >> a[i];
        pq.push({calc(d[i]) * a[i] , i});
    }
    int cnt = n - 2;
    while (cnt--) {
        auto [val, idx] = pq.top(); pq.pop();
        d[idx]++;
        pq.push({calc(d[idx]) * a[idx], idx});
    }
    ll ans = 0;
    for (int i = 1; i <= n; i++)
        ans += d[i] * d[i] * a[i];
    cout << ans << endl;
    return 0;
}

G - Sum of Tree Distance

Question

给定一棵 $N$ 个节点的树。第 $i$ 条边双向连接节点 $u_i$ 和 $v_i$。

此外，还给出一个整数序列 $A=(A_1,\ldots,A_N)$。

这里，定义 $f(i,j)$ 如下：

• 如果 $A_i = A_j$，那么 $f(i,j)$ 是从节点 $i$ 到节点 $j$ 移动所需的最小边数。如果 $A_i \neq A_j$，则 $f(i,j) = 0$。

计算以下表达式的值：

$\displaystyle \sum_{i=1}^{N-1}\sum_{j=i+1}^N f(i,j)$

Solution

设定一个分界点 $B=\sqrt{n}$

• 如果一种颜色的数量 $cnt \le B$，那么直接暴力求 $LCA$ 即可，注意要用 $O(1)$ 求 $LCA$ 的方法

• 如果一种颜色的数量 $cnt > B$，因为这样子的颜色种类很少最多 $\frac{n}{B}$ 个，所以考虑 $O(n)$ 的 DFS 来求，也不会超时

总时间复杂度为 $O(n\sqrt{n})$

Code

#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> g;
vector<int> A;
typedef long long ll;
const int maxn = 2e5 + 5;
int dep[maxn << 1], lg[maxn << 1], st[maxn << 1][25], dfn[maxn], tot;
int E[maxn << 1];

void dfs (int u, int fa) {
    dfn[u] = ++tot; E[tot] = u;
    dep[u] = dep[fa] + 1;
    for (auto v : g[u]) {
        if (v == fa) continue;
        dfs(v, u);
        E[++tot] = u;
    }
}

void build_st() {
    lg[0] = -1;
    for (int i = 1; i <= tot; i++)
        lg[i] = lg[i >> 1] + 1;
    for (int i = 1; i <= tot; i++)
        st[i][0] = E[i];
    for (int j = 1; j <= 20; j++) {
        for (int i = 1; i + (1 << j) - 1 <= tot; i++) {
            int x = st[i][j - 1], y = st[i + (1 << (j - 1))][j - 1];
            st[i][j] = dep[x] < dep[y] ? x : y;
        }
    }
}

int lca (int u, int v) {
    if (dfn[u] > dfn[v]) swap(u, v);
    int l = dfn[u], r = dfn[v];
    int k_ = lg[r - l + 1];
    int x = st[l][k_], y = st[r - (1 << k_) + 1][k_];
    return dep[x] < dep[y] ? x : y;
}

int dist (int u, int v) {
    return dep[u] + dep[v] - 2 * dep[lca(u, v)];
}

ll now, all;

void dfs_1 (int u, int fa, int col, vector<int> &siz) {
    siz[u] = 0;
    for (auto v : g[u]) {
        if (v == fa) continue;
        dfs_1(v, u, col, siz);
        siz[u] += siz[v];
    }
    if (A[u] == col) {
        siz[u] += 1;
    }
    now += 1ll * (all - siz[u]) * siz[u];
}



int main() {
    ios::sync_with_stdio(0);
    int n; cin >> n;
    g.assign(n + 1, vector<int>());
    for (int i = 1; i < n; i++) {
        int u, v; cin >> u >> v;
        g[u].push_back(v); g[v].push_back(u);
    }
    A.assign(n + 1, 0);
    vector<vector<int>> p(n + 1, vector<int>());
    for (int i = 1; i <= n; i++) {
        cin >> A[i];
        p[A[i]].push_back(i);
    }

    dfs(1, 0);
    build_st();

    const int B = sqrt(n);
    ll ans = 0;
    vector<int> siz(n + 1, 0);
    vector<ll>  R(n + 1, 0);
    for (auto &v : p) {
        if (v.empty()) continue;
        int col = A[v[0]]; now = 0, all = v.size();
        if (v.size() <= B) {
            for (int i = 0; i < v.size(); i++)
                for (int j = i + 1; j < v.size(); j++)
                    now += dist(v[i], v[j]);
        }
        else {
            dfs_1(1, 0, col, siz);
        }
        ans += now;
    }
    cout << ans << endl;
    return 0;
}