 线段树
线段树
# 线段树
线段树可以理解为 “分治法思想+二叉树结构+Lazy-Tag 技术”
线段树一颗二叉树,树上的结点是 “线段”,线段是根据分治法得到的
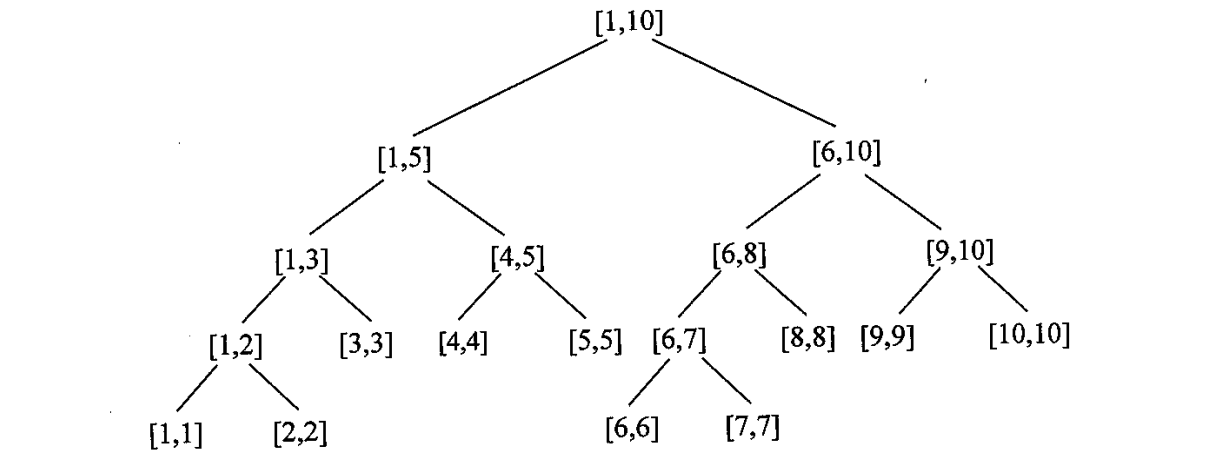
每个结点上可以存放一些信息,例如最值,加和,乘积等等
结合分治的思想,线段树适合解决的问题的特征是:大区间的解可以从小区间的解合并而来
# 基本操作
# 构造
我们先使用静态的方法来构造线段树,有点是父节点和子节点之间的访问很简单,缺点是最后一行有大量结点被浪费
struct Segment_Tree{
vector<int> t;
Segment_Tree(int n){t.resize(n << 2);}
void push_up(int x){
t[x] = t[x<<1] + t[x<<1|1];
}
void build(int x, int l, int r, vector<int>& a){
if(l == r) {t[l] = a[l]; return ;}
int mid = (l + r) >> 1;
build(x << 1, l, mid, a); build(x << 1 | 1, mid + 1, r ,a);
push_up(x);
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 区间查询
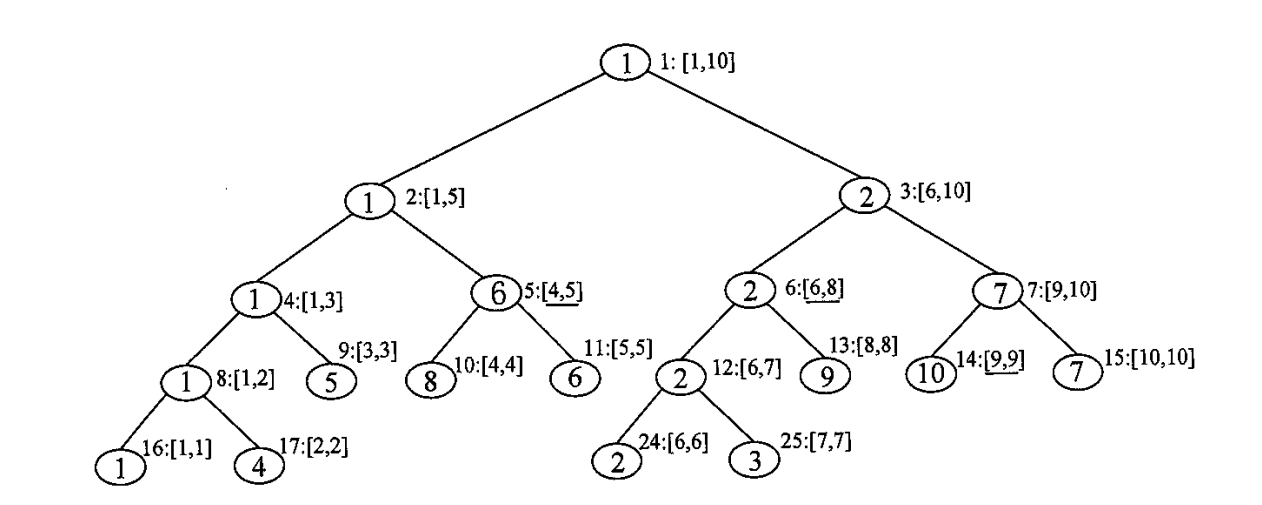
我们以求区间最小值为例,我们能把区间分成不超过 个小区间的 "加和",例如区间 可以分成 ,我们可以使用递归来找到这些小区间
这段代码是求区间和的
int query(int x, int l, int r, int ql, int qr){
if(ql <= l && r <= qr) return t[x];
int mid = (l + r) >> 1, ret = 0;
if(ql <=mid) ret += query(x << 1, l, mid, ql, qr);
if(qr > mid) ret += query(x << 1 | 1, mid + 1, r, ql, qr);
return ret;
}
2
3
4
5
6
7
# Lazy-Tag
考虑区间修改+区间查询
对于 内的每个数,我们一个一个单点修改,则 次的时间复杂度为
很容易可以想到,我们可以对于一个线段树的结点 ,定义 统一来记录区间 的操作,而不是一个一个地修改区间内的每个元素,这个方法被称为 懒标记操作
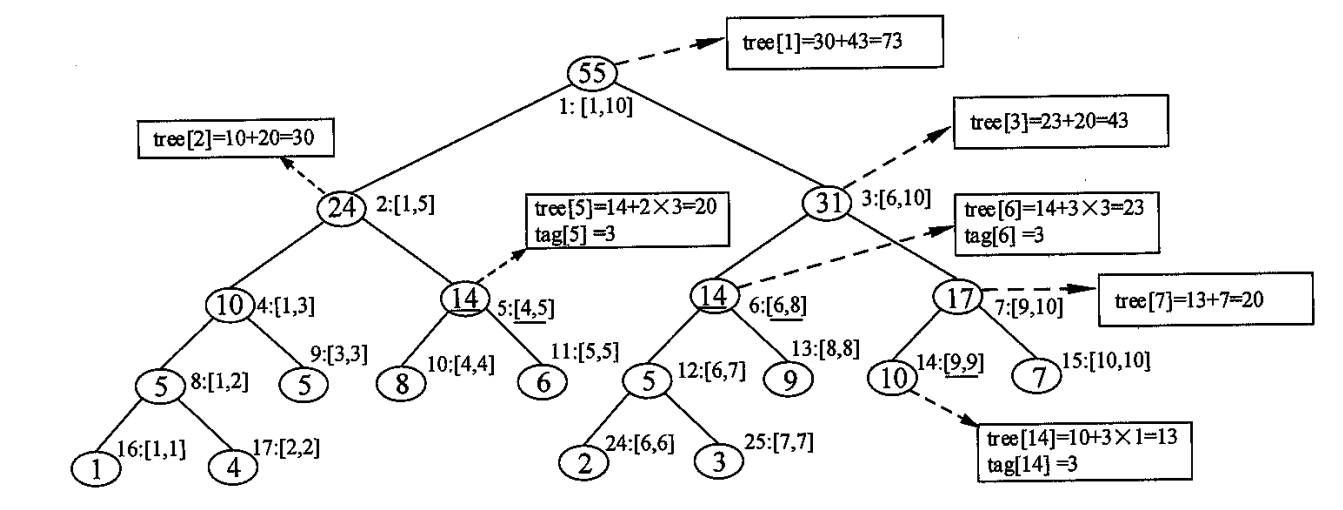
例如,我们想要把 内的所有元素加 ,步骤如下
- 左子树递归到结点 ,即区间 ,修改 ,然后打标记
- 右子树递归到结点 ,即区间 ,修改 ,然后打标记
注意,每次要先修改这个结点的值,然后打上标记,表示这个子树的儿子没有被修改过
当我们再次遍历到这个元素的时候,就需要把标记往下传,就需要使用到 函数
具体操作就是,如果 结点的 如果有值,那么把修改左右儿子,然后把 传给左右儿子
struct Seg_Tree{
int n;
vector<int> t,tag;
Seg_Tree(int n){this->n=n;t.assign(n<<2,0);tag.assign(n<<2,0);}
void push_up(int x){t[x]=t[x<<1]+t[x<<1|1];}
void build(int x,int l,int r,vector<int>& a){
if(l==r) {t[x]=a[l];return ;}
int mid=(l+r)>>1;
build(x<<1,l,mid,a);build(x<<1|1,mid+1,r,a);
push_up(x);
}
void add_tag(int x,int l,int r,int val){
t[x]+=val*(r-l+1);
tag[x]+=val;
}
void push_down(int x,int l,int r){
if(tag[x]){
int mid=(l+r)>>1;
add_tag(x<<1,l,mid,tag[x]);
add_tag(x<<1|1,mid+1,r,tag[x]);
tag[x]=0;
}
}
void update(int x,int l,int r,int ql,int qr,int val){
if(ql<=l&&r<=qr){ //完全覆盖,给这个结点打上 tag 不用深入了
add_tag(x,l,r,val);
return ;
}
push_down(x,l,r);
int mid=(l+r)>>1;
if(ql<=mid) update(x<<1,l,mid,ql,qr,val);
if(qr>mid) update(x<<1|1,mid+1,r,ql,qr,val);
push_up(x);
}
int query(int x,int l,int r,int ql,int qr){
if(ql<=l&&r<=qr) return t[x];
push_down(x,l,r);
int mid=(l+r)>>1,ret=0;
if(ql<=mid) ret+=query(x<<1,l,mid,ql,qr);
if(qr>mid) ret+=query(x<<1|1,mid+1,r,ql,qr);
return ret;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
对于区间修改+区间查询线段树和树状数组都能实现,但是一般都用线段树实现,因为树状数组难写且局限很大
# 区间最值和历史最值
没怎么懂说实话,插个眼过几天看
# 线段树合并
我们发现,线段树相邻的结点之间所表示的“区间” 也相邻,我们就能用这个性质来维护一些东西
# 扫描线
扫描线算法是线段树的经典应用,他能解决矩形面积并,多边形面积等几何问题
考虑区间并
我们可以把几个矩形转化一下,例如:我们可以把两个大的矩形转换成三个新的矩形
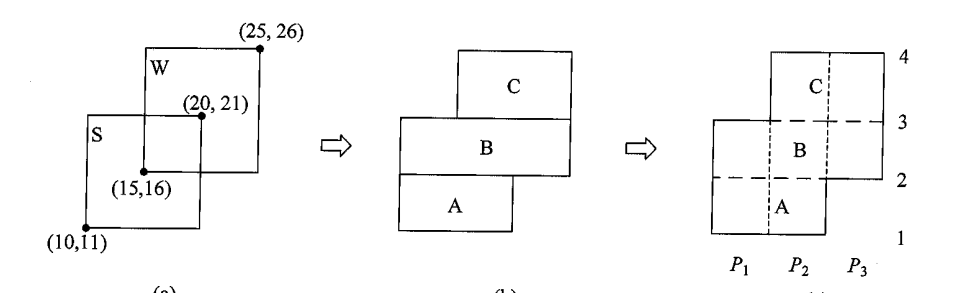
对于每个矩形,其面积 宽 高
然后我们定义入边和出边的概念,对于每一条横边,一个矩形从下往上的第一条边叫做入边,第二条边叫做出边
我们按照竖边把横边分块,例如图中有 条竖边,就分成了 , 个块,对于每个块,我们可以记录它被入边覆盖了几次,被出边覆盖了几次,定义入边为 ,出边为 ,记录这个块当前的总和为 ,如果这个块的 那么这个块在此时是被覆盖的
用线段树来维护每个块的 ,和每个块的 ,然后累计答案就是对于每一条横边,累计上所有 的块的高度 这一个横边到上一个横边的纵向距离
线段树维护时要注意,实际上线段树维护的区间范围要比竖边的数量小 ,例如:第一个竖边和第二个竖边的那段长度被线段树的 号位置维护,写代码时要注意这个细节
#include<bits/stdc++.h>
using namespace std;
struct Scan_Line{
double y; /// 边 y 的坐标
double left_x,right_x; // 边的右端点和左端点
int op; // 1 表示入边 -1 表示出边
Scan_Line(double y=0,double left_x=0,double right_x=0,int op=0):y(y),left_x(left_x),right_x(right_x),op(op){}
};
vector<double> xx;
bool cmp(Scan_Line a,Scan_Line b){return a.y<b.y;} //按照 y 坐标从小到大排序
struct Segment_Tree{
int n;
vector<double> t;
vector<int> sum;
Segment_Tree(int n){this->n=n;t.assign(n<<2,0);sum.assign(n<<2,0);}
void push_up(int x,int l,int r){
if(sum[x]) t[x]=xx[r+1]-xx[l];
else if(l==r) t[x]=0;
else t[x]=t[x<<1]+t[x<<1|1];
}
void update(int x,int l,int r,int ql,int qr,int val){
if(ql<=l&&r<=qr){sum[x]+=val;push_up(x,l,r);return ;}
int mid=(l+r)>>1;
if(ql<=mid) update(x<<1,l,mid,ql,qr,val);
if(qr>mid) update(x<<1|1,mid+1,r,ql,qr,val);
push_up(x,l,r);
}
};
int main(){
int n,cas=0;
while(scanf("%d",&n),n){
int cnt=0;
vector<Scan_Line> lines(2*n+1);
xx.assign(2*n+1,0);
for(int i=1;i<=n;i++){
double x1,x2,y1,y2;scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
lines[++cnt]=Scan_Line(y1,x1,x2,1);
lines[++cnt]=Scan_Line(y2,x1,x2,-1);
xx[cnt-1]=x1;xx[cnt]=x2;
}
sort(xx.begin()+1,xx.begin()+cnt+1);
int num=unique(xx.begin()+1,xx.begin()+cnt+1)-(xx.begin()+1);//去重,离散化
Segment_Tree T(num);
sort(lines.begin()+1,lines.begin()+cnt+1,cmp);
double ans=0;
for(int i=1;i<=cnt;i++){
int L,R;
ans+=T.t[1]*(lines[i].y-lines[i-1].y);
L=lower_bound(xx.begin()+1,xx.begin()+num+1,lines[i].left_x)-xx.begin();
R=lower_bound(xx.begin()+1,xx.begin()+num+1,lines[i].right_x)-xx.begin();
T.update(1,1,num,L,R-1,lines[i].op);
}
printf("Test case #%d\nTotal explored area: %.2lf\n\n",++cas,ans);
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
# 可持久化线段树
可持久化线段树也叫主席树,有些时候,我们需要记录”不同时间点“的数据状态,最暴力的想法就是建很多棵线段树,但是实际上我们发现,实际上在相邻的时间点的两颗线段树的区别很小,从一颗线段树开始,我们只需要改动一点点就可以得到另外一个线段树了。这样的数据结构就要可持久化数据结构
考虑一个经典的问题:区间第 大/小问题
给定 个整数构成的序列 ,对指定的序列闭区间 查询区间内的第 小值
能否用线段树解决,线段树适合处理区间问题,区间和,区间最值,这些问题都有一个共同点,就是大区间可以由小区间组合而来。然而,区间第 大问题并不满足这种特征,所以无法直接使用线段树
我们考虑使用可持久化线段树,建立 棵权值线段树分别表示 的数字出现的次数
例如:原序列为 ,在离散后变成了 ,然后建树
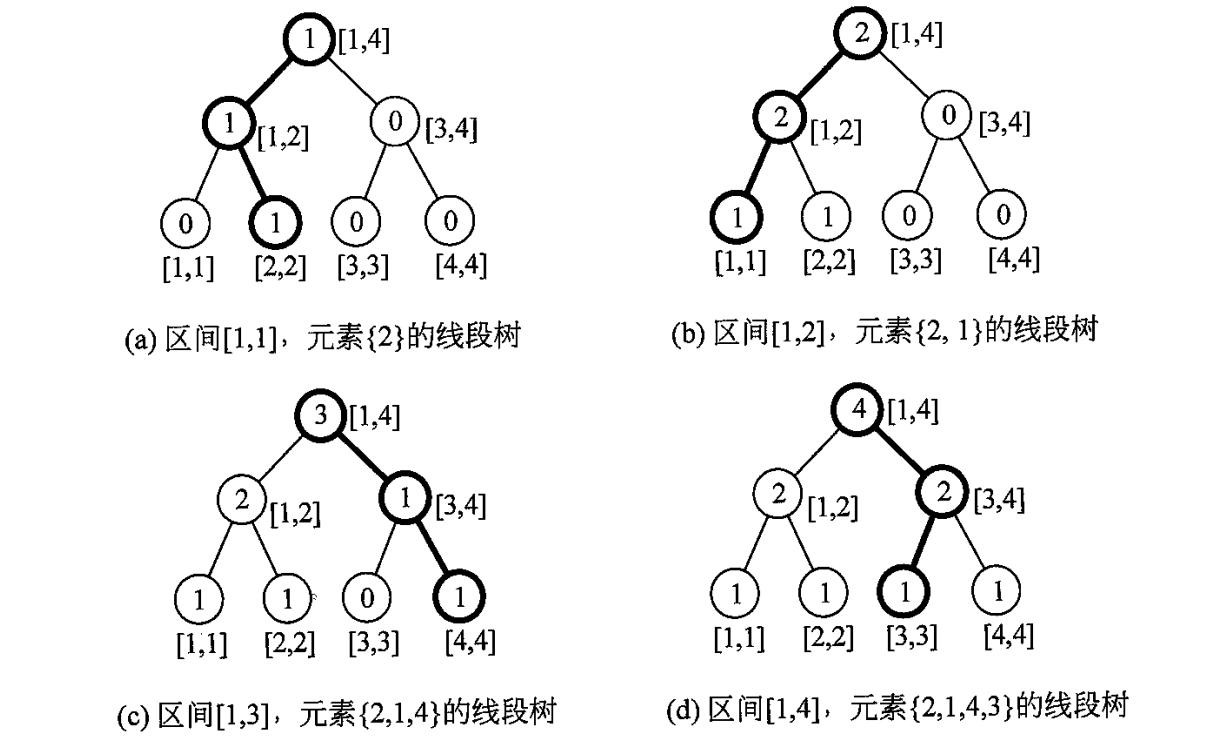
我们发现,每棵线段树与上一棵树的不同只在于粗线上的结点,是一条链
考虑如何求 的第 大数字,就是从根结点开始走,如果左节点 那么说明第 大的在左结点,否则就在右节点
拓展到如何求 的第 大数字,利用差分的思想,对于每个结点,我们把 那棵子树 - 那棵子树所对应的结点,最后得到的树就是 区间所对应的权值线段树
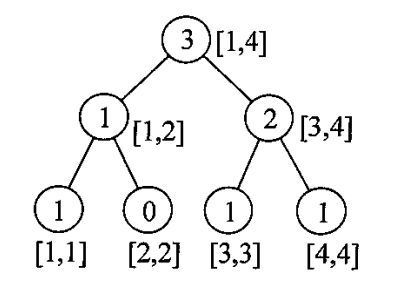
每棵线段树的结点个数是 的,那么每次查询的复杂度也是 的,实际上,我们只需要对查询路径上的那些结点做减法就好了,所以每次查询的复杂度是
考虑空间复杂度,如果要建 棵树,那么总共需要 的空间,观察这 棵线段树,相邻的两棵树只有一条链上是不同的,那么就意味着,相邻的树之间可以共用结点
初始先建一颗原始空树,它是一颗完整的线段树,然后开始建第一颗树,它只在空树上修改了 个结点,只新建 个结点即可,然后这三个结点指向没修改的部分也就是指向原来空树上的其他子节点
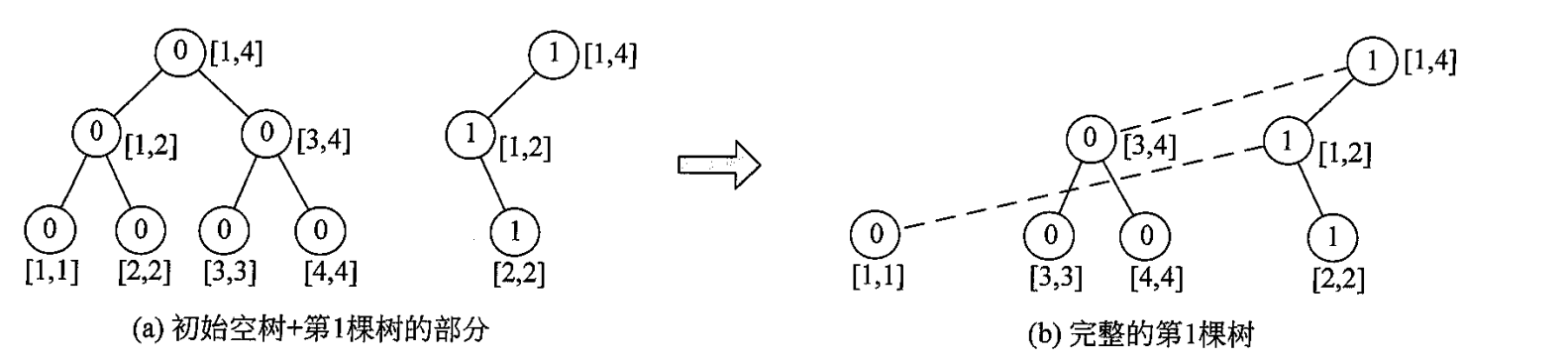
建其他树时,也同理,新建 个结点,并把新建的结点指向前一颗线段树的子节点 ,一共建立了 棵线段树,每颗线段树有 个结点,所以总空间复杂度为 ,实际编码时,一般开
在具体代码实现时,有些细节可以这样处理
如何定位每颗线段树?定义 数组记录每颗线段树的根结点
事实上,原始空树的每个结点的值都为 ,所以, 就没有必要去建立原始空树,即节省空间还节省时间
对于重复元素,我们去重后的数字个数为 ,也就是说,原始空树的是基于 建的,但实际上我们开空间还是需要
#include<bits/stdc++.h>
using namespace std;
struct Node{
int lson,rson,sum;
Node(int lson=0,int rson=0,int sum=0) {this->lson=lson;this->rson=rson;this->sum=sum;}
};
struct Segment_Tree{
int n,cnt;
vector<Node> t;
Segment_Tree(int n){this->n=n;t.assign(n<<5,Node());cnt=0;}
int update(int pre,int l,int r,int pos){
int now=++cnt; //动态开点
t[now].lson=t[pre].lson; t[now].rson=t[pre].rson; t[now].sum=t[pre].sum+1; //复制 lson,rson,sum 比原来的多 1
int mid=(l+r)>>1;
if(l<r){
if(pos<=mid) t[now].lson=update(t[pre].lson,l,mid,pos); //继续往左边走
else t[now].rson=update(t[pre].rson,mid+1,r,pos); //继续往右边走
}
return now;
}
int query(int u,int v,int l,int r,int k){ //[u,v] 内第 k 小数,相当于同时在两棵树上面走
if(l==r) return l;// 返回第 k 小的数字的编号
int now_lson_x=t[t[v].lson].sum-t[t[u].lson].sum; // 两棵线段树相减,得到左边儿子在 [u,v] 的个数
int mid=(l+r)>>1;
if(now_lson_x>=k)
return query(t[u].lson,t[v].lson,l,mid,k); //在左边儿子
else
return query(t[u].rson,t[v].rson,mid+1,r,k-now_lson_x); //在右边儿子
}
};
int main(){
freopen("P3834.in","r",stdin);
int n,m;scanf("%d%d",&n,&m);
vector<int> a(n+1),b(n+1),rt(n+1,0);
for(int i=1;i<=n;i++) {scanf("%d",&a[i]);b[i]=a[i];} //b 为 a 的副本
sort(b.begin()+1,b.begin()+1+n);
int num=unique(b.begin()+1,b.begin()+1+n)-(b.begin()+1);
Segment_Tree T(n); //这里不能填num,因为每次新建的结点个数时 logn 的一共有 nlogn
for(int i=1;i<=n;i++){
int x=lower_bound(b.begin()+1,b.begin()+1+num,a[i])-b.begin(); // x 为离散化后的 a[i] 的值
rt[i]=T.update(rt[i-1],1,num,x);
}
while(m--){
int L,R,k;scanf("%d%d%d",&L,&R,&k);
int id=T.query(rt[L-1],rt[R],1,num,k);
printf("%d\n",b[id]);
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
# 李超线段树
# 实现
李超线段树一般用来解决线段交集凸包问题:
- 加入一个一次函数,定义域为
- 给定 ,求定义域包含 的所有一次函数中,在 处取值最大的那个,如果有多个函数取值相同,选编号最小的
看到区间修改,我们按照线段树解决区间问题的常见方法,给每个节点一个懒标记,每个节点 的懒标记都是一条线段,记为 ,表示要用 更新该节点所表示的整个区间
考虑现在要插入一条新的线段
第一步要按照线段树的常规方法找到被 完整覆盖的区间
第二步是修改区间内的懒标记,具体如何如何修改?
考虑一个区间的懒标记原来的值为 ,若原来没有值,则直接为
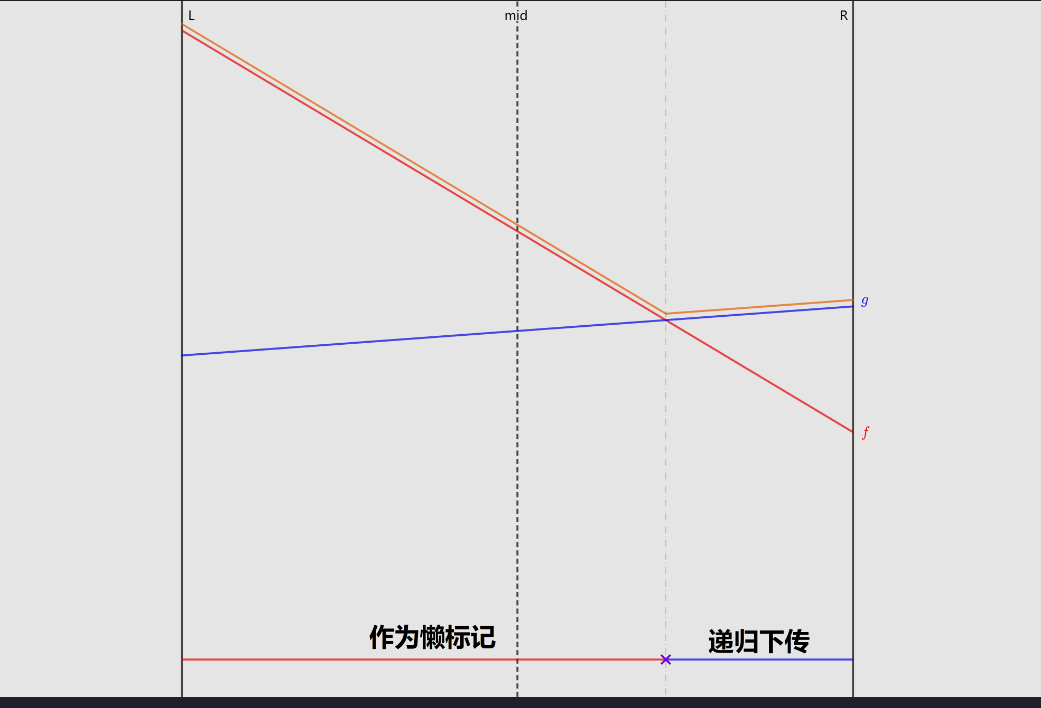
不妨假设 在区间中点处比 更大的情况(若比 小,交换 即可)
- 若在左端点处 更优,那么 和 必然在左儿子内相交,递归更新左儿子
- 若在右端点处 更优,那么 和 必然在右儿子内相交,递归更新右儿子
- 若左右端点处 都更优,那么 不可能成为答案,则不需要下传
除了这两种情况之外,还有一种情况是 和 正好相较于中点,在程序实现时可以归入中点不如 的情况,依旧会更新一边
考虑时间复杂度,线段树最多把区间分成 个小区间,每个小区间更新的时间复杂度时 ,总时间复杂度为
# 例题
P4097 【模板】李超线段树 / [HEOI2013] Segment (opens new window) 要求在平面直角坐标系下维护两个操作
- 在平面上加入一条线段,记第 条被插入的线段的标号为
- 给定一个数 询问与直线 相交的线段中,交点纵坐标最大的线段编号
强制在线
#include <bits/stdc++.h>
using namespace std;
const int mod1 = 39989, mod2 = 1e9;
const double eps = 1e-9;
typedef pair<double, int> pdi;
int cmp(double x, double y) {
if (fabs(x - y) < eps) return 0;
if (x < y) return -1;
return 1;
}
struct Line {
int id;
double k, b;
Line() {k = 0, b = 0; id = 0;}
Line(int x_0, int y_0, int x_1, int y_1, int id) {
this->id = id;
if (x_0 == y_0) k = 0, b = max(y_0, y_1);
else k = 1.0 * (y_1 - y_0) / (x_1 - x_0), b = y_0 - k * x_0;
}
double calc(int x) { return k * x + b;}
};
bool operator < (const pdi &a, const pdi &b) {
if (cmp(a.first, b.first) == 0) return a.second > b.second;
return a.first < b.first;
}
pdi max (const pdi &a, const pdi &b) {
return a < b ? b : a;
}
int max_x = 0;
struct Segment_Tree {
int n;
vector<Line> t;
Segment_Tree (int n) {
this->n = n;
t.resize(4 * n);
}
void upd_line (int x, int l, int r, Line v) {
max_x = max(max_x, x);
auto &u = t[x];
int mid = (l + r) / 2;
int op_mid = cmp(v.calc(mid), u.calc(mid));
if (op_mid == 1 || (op_mid == 0 && v.id < u.id)) swap(u, v);
if (l == r) return;
int op_le = cmp(v.calc(l), u.calc(l)), op_ri = cmp(v.calc(r), u.calc(r));
if (op_le == 1 || (op_le == 0 && v.id < u.id))
upd_line (x << 1, l, mid, v);
if (op_ri == 1 || (op_ri == 0 && v.id < u.id))
upd_line (x << 1 | 1, mid + 1, r, v);
}
void upd_pos (int x, int l, int r, int ql, int qr, Line v) {
max_x = max(max_x, x);
if (ql <= l && r <= qr) {
upd_line (x, l, r, v);
return;
}
int mid = (l + r) / 2;
if (ql <= mid) upd_pos (x << 1, l, mid, ql, qr, v);
if (qr > mid) upd_pos (x << 1 | 1, mid + 1, r, ql, qr, v);
}
pdi query (int x, int l, int r, int pos) {
max_x = max(max_x, x);
if (l == r) return pdi(t[x].calc(pos), t[x].id);
int mid = (l + r) / 2;
pdi res = pdi(t[x].calc(pos), t[x].id);
if (pos <= mid) res = max(res, query(x << 1, l, mid, pos));
else res = max(res, query(x << 1 | 1, mid + 1, r, pos));
return res;
}
};
int main() {
freopen ("P4097.in", "r", stdin);
freopen ("P4097.out", "w", stdout);
int n; cin >> n;
int lastans = 0, cnt = 0;
Segment_Tree T (mod1 + 1);
for (int i = 1; i <= n; i++) {
int op; cin >> op;
if (op == 0) {
int x; cin >> x;
x = (x + lastans - 1) % mod1 + 1;
// cout << x << endl;
lastans = T.query(1, 1, mod1, x).second;
cout << lastans << endl;
}
else {
int x_0, x_1, y_0, y_1; cin >> x_0 >> y_0 >> x_1 >> y_1;
x_0 = (x_0 + lastans - 1) % mod1 + 1, x_1 = (x_1 + lastans - 1) % mod1 + 1;
y_0 = (y_0 + lastans - 1) % mod2 + 1, y_1 = (y_1 + lastans - 1) % mod2 + 1;
// cout << x_0 << " " << y_0 << " " << x_1 << " " << y_1 << endl;
if (x_0 > x_1) swap(x_0, x_1), swap(y_0, y_1);
T.upd_pos(1, 1, mod1, x_0, x_1, Line(x_0, y_0, x_1, y_1, ++cnt));
}
}
// cout << max_x << endl;
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
