机器学习笔记

前言

监督学习

回归问题

有监督学习中，你的训练集存在一个输入数据 $x$ 和一个正确的答案 $y$，算法根据训练集训练，然后给出一个位置的 $x$ 来预测一个新的 $y$

这里我们根据 $x$，从无数个数中预测

分类问题

上面的回归问题是从无数的数中预测一个 $y$，分类问题是根据训练数据训练算法，然后对于一个新的 $x$，把这个 $x$ 分到规定的几类中

例如：根据肿瘤的大小来判断肿瘤是恶性的还是良性的

无监督学习

无监督学习对于数据 $x$ 不会给出对应的正确输出 $y$，需要程序自己去发现数据中一些特殊的结构或者规律

聚类算法

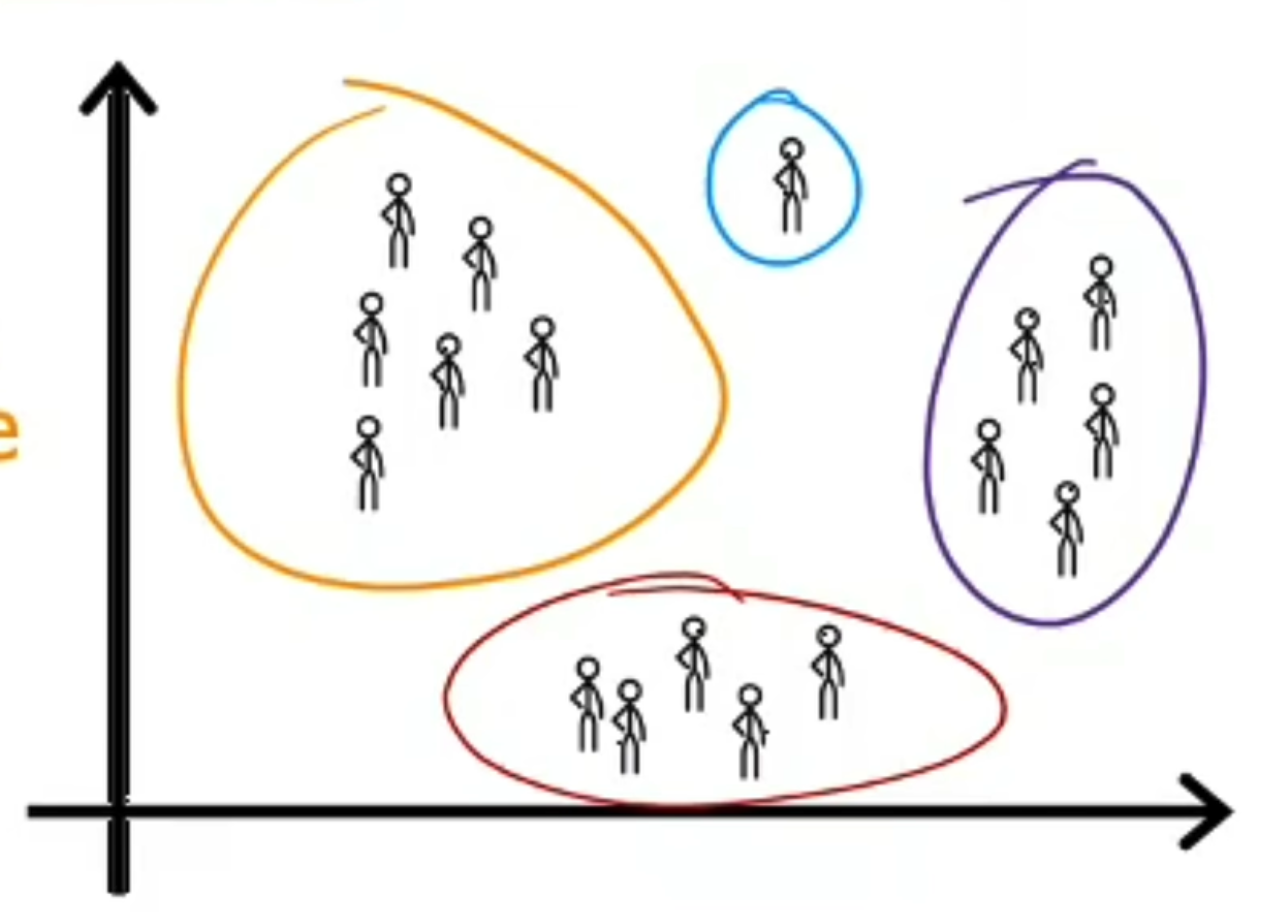
在图中，我们可以发现一类人有相似的一些特征，所以我们把他们归为一类

Anomaly detection

异常值检测

线性回归

一元线性回归

观察一条直线，$y=\beta_0+\beta_1 x$，我们给定一个 $x$ 就能得到一个 $y$

当我们用一个 $x$ 来预测 $y$，就是一元线性回归模型

我们现在有一堆数据集 $(x,y)$，然后我需要找到合适的 $\beta_0,\beta_1$ 来拟合这些点

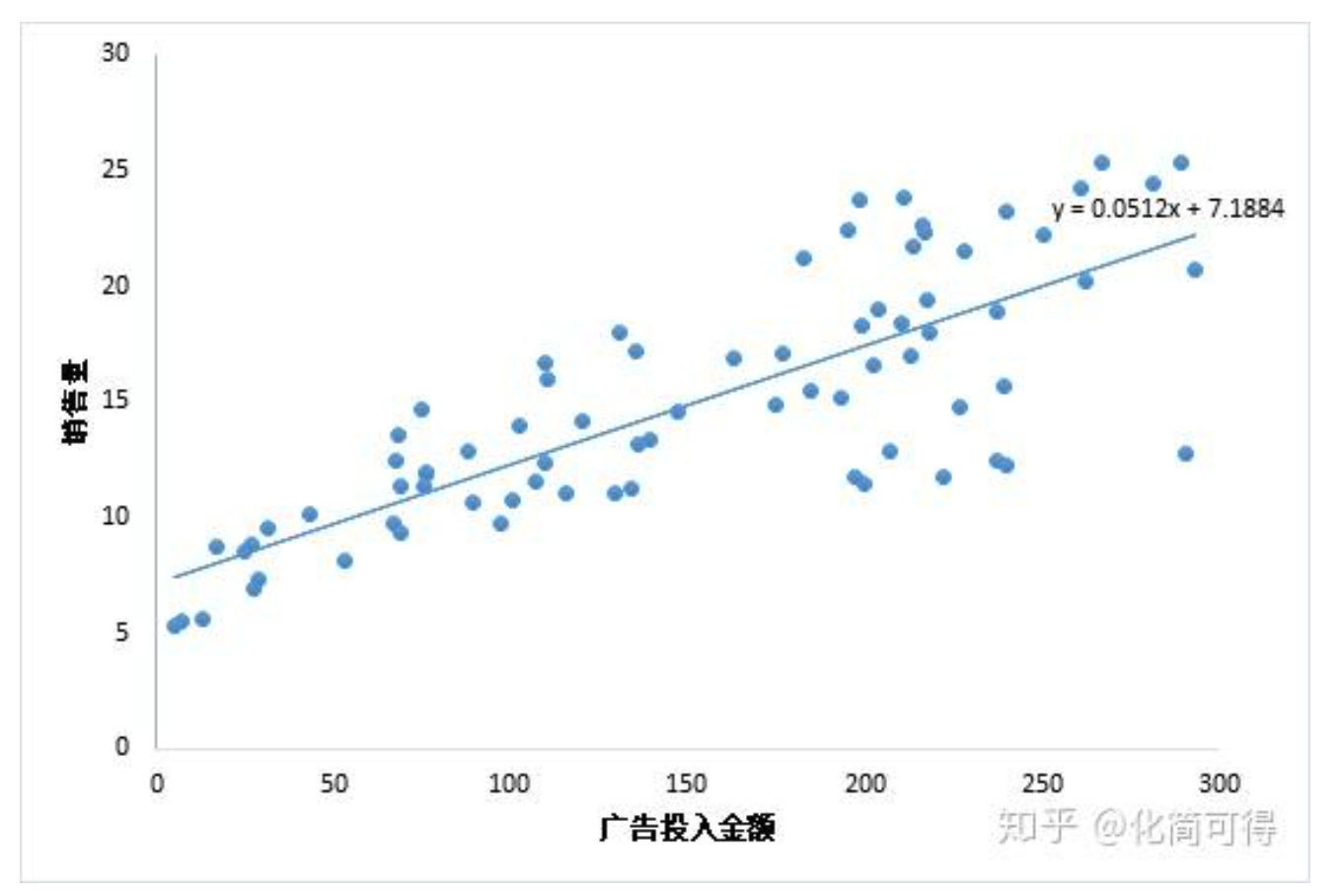
于是，当来了一个新的 $x$，就能得到一个 $y$ 了

我们需要一个评价标准来评判一条直线的拟合程度，于是就有了损失函数

定义真实值和预测值之间的差值为残差：$e=y-\hat{y}$

那么误差就是残差平方和，叫 损失函数

$Q=\sum_{i=1}^m (y_i-\hat{y_i})^2=\sum_{i=1}^m (y_i-(\hat\beta_0+\hat{\beta_1x_i}))^2$

我们的目标就是需要找到最小化 $Q$，即：

$(w^*,b^*)=\arg\min\sum_{i=1}^n (f(x_i)-y_i)^2=\arg\min\sum_{i=1}^n (y_i-wx_i-b)^2$

求解 $w$ 和 $b$ 使得 $E_{(w,b)}=\sum_{i=1}^n (y_i-wx_i-b)^2$ 被称为最小二乘估计，对 $E_{(w,b)}$ 分别求偏导数，得到：

$\begin{aligned} \frac{\partial E_{(w,b)}}{\partial w} &=2\left( w\sum_{i=1}^m x^2-\sum_{i=1}^m (y_i-b)x_i\right)\\ \frac{\partial E_{(w,b)}}{\partial w} &= 2\left( mb-\sum_{i=1}^m(y_i-wx_i)\right) \end{aligned}$

两个偏导数等于 $0$ 就可以得到 $w$ 和 $b$ 对最优解

$w=\frac{\sum_{i=1}^m y_i(x_i-\overline{x})}{\sum_{i=1}^m x^2-\frac{1}{m}\left(\sum_{i=1}^m x_i \right)^2}$

$b=\frac{1}{m}\sum_{i=1}^m (y_i-wx_i)$

其中 $\overline{x} =\frac{1}{m}\sum_{i=1}^m x_i$ 为 $x$ 的均值

多元线性回归

给定数据集 $D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)\}$，其中 $x_i=(x_{i1},x_{i2},\cdots,x_{id}),y\in \mathbb{R}$，这里的 $x_i$ 是一个向量的形式，我们试图得到一个矩阵 $w,b$

$f(x_i)=w^Tx_i+b$

类似的，我们可以用最小二乘法来对 $w$ 和 $b$ 进行估计，我们把 $w,b$ 写成一个 $\hat{w}=(w;b)$，把数据集表示成一个 $m\times (d+1)$ 大小大矩阵 $X$，其中每一行对应一个示例，最后一个元素恒为 $1$ $$ \mathbf{X}=\left(\begin{array}{ccccc} x_{11} & x_{12} & \ldots & x_{1 d} & 1 \ x_{21} & x_{22} & \ldots & x_{2 d} & 1 \ \vdots & \vdots & \ddots & \vdots & \vdots \ x_{m 1} & x_{m 2} & \ldots & x_{m d} & 1 \end{array}\right)=\left(\begin{array}{cc} \boldsymbol{x}{1}^{\mathrm{T}} & 1 \ \boldsymbol{x}{2}^{\mathrm{T}} & 1 \ \vdots & \vdots \ \boldsymbol{x}_{m}^{\mathrm{T}} & 1 \end{array}\right) $$

把标记也写成向量形式 $y=(y_1,y_2,\cdots,y_m)$，那么多位的损失函数就可以写成：

$\hat{w}^*=\arg\min(y-X\hat{w})^T(y-X\hat{w})$

令 $E_{\hat{w}}=(y-X\hat{w})^T(y-X\hat{w})$，对 $\hat{w}$ 求导得到

$\frac{\partial E_{\hat{w}}}{\partial \hat{w}} = 2X^T(X\hat{w}-y)$

当 $X^T X$ 为满秩矩阵或正定矩阵时

$\hat{w}^*=(X^TX)^{-1}X^Ty$

令 $\hat{x_i}=(x_i,1)$ 可得，多元线性回归模型为

$f(\hat{x_i})=\hat{x_i}^T (X^TX)^{-1}X^Ty$

使用梯度下降求解多元线性回归

考虑单变量的线性回归中，我们考虑每次迭代 $w$ 和 $b$，方程如下 $$ \begin{aligned} w&=w-\alpha \frac{\partial}{\partial w} J(w,b)=w-\alpha \frac{1}{m}\sum_{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})x^{i}\ b&=b-\alpha \frac{\partial}{\partial b} J(w,b)=b-\alpha \frac{1}{m}\sum_{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}) \end{aligned} $$ 在多元线性回归中，$\vec{x}$ 和 $\vec{v}$ 都是一个向量，所以，上面那个方程需要做一些改变 $$ \begin{aligned} w_1&=w_1-\alpha \frac{\partial}{\partial w} J(w,b)=w_1-\alpha \frac{1}{m}\sum_{i=1}^m(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})x^{i}1\ \cdots\ w_n&=w_n-\alpha \frac{\partial}{\partial w} J(w,b)=w_n-\alpha \frac{1}{m}\sum{i=1}^m(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})x^{i}n\ b&=b-\alpha \frac{\partial}{\partial b} J(w,b)=b-\alpha \frac{1}{m}\sum{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}) \end{aligned} $$

梯度下降

假设你有一个代价函数 $J(w,b)$，你需要找到 $\min_{w,b}J(w,b)$

基本算法思想是：

• 给 $w,b$ 一个初始，通常是 $w=0,b=0$
• 稍微改变一点 $w,b$ 来减少 $J(w,b)$
• 直到 $J$ 稳定在最小值附近

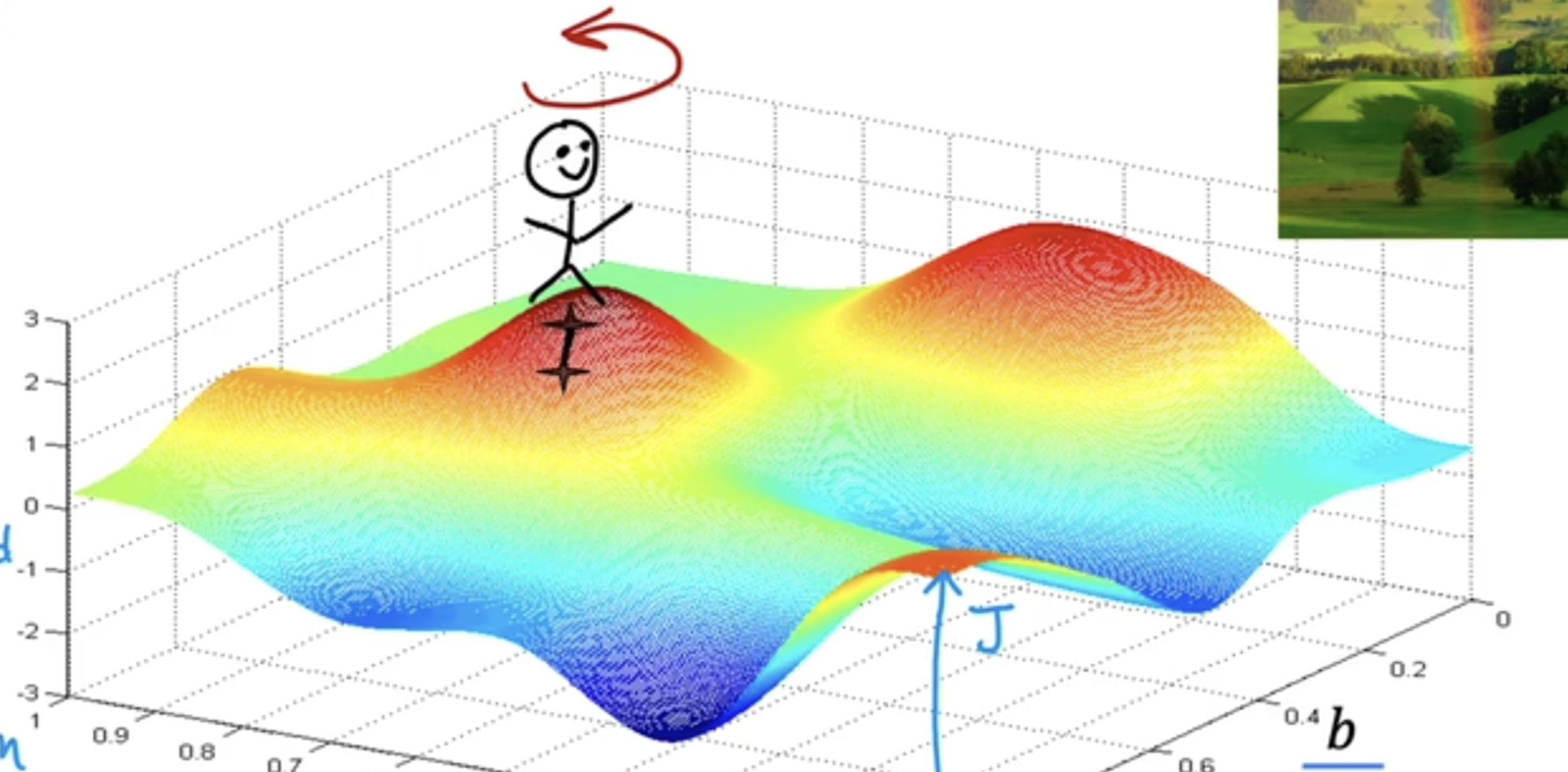
假设你站在这个山顶上，你要往前试探性的走一步，然后看往那个方向走能让你更快得降到山谷中，然后就往那个方向走一步，以此类推

接下来我们来看一下如何具体实现梯度下降算法，这里实现了 $w,b$ 的同时更新 $$ \begin{aligned} w&=w-\alpha \frac{\partial}{\partial w} J(w,b)\ b&=b-\alpha \frac{\partial}{\partial b} J(w,b) \end{aligned} $$

• 这里的 $\alpha$ 是学习率，其决定了梯度下降的步伐大小

如果学习率 $\alpha$ 特别小，梯度下降算法会起作用，但是需要很长的时间

如果学习率 $\alpha$ 太大，梯度下降算法可能无法找到最小值

检查梯度下降是否收敛

我们将梯度下降的次数为横轴，$J(\vec{w,b})$ 为纵轴，花了一个图

​

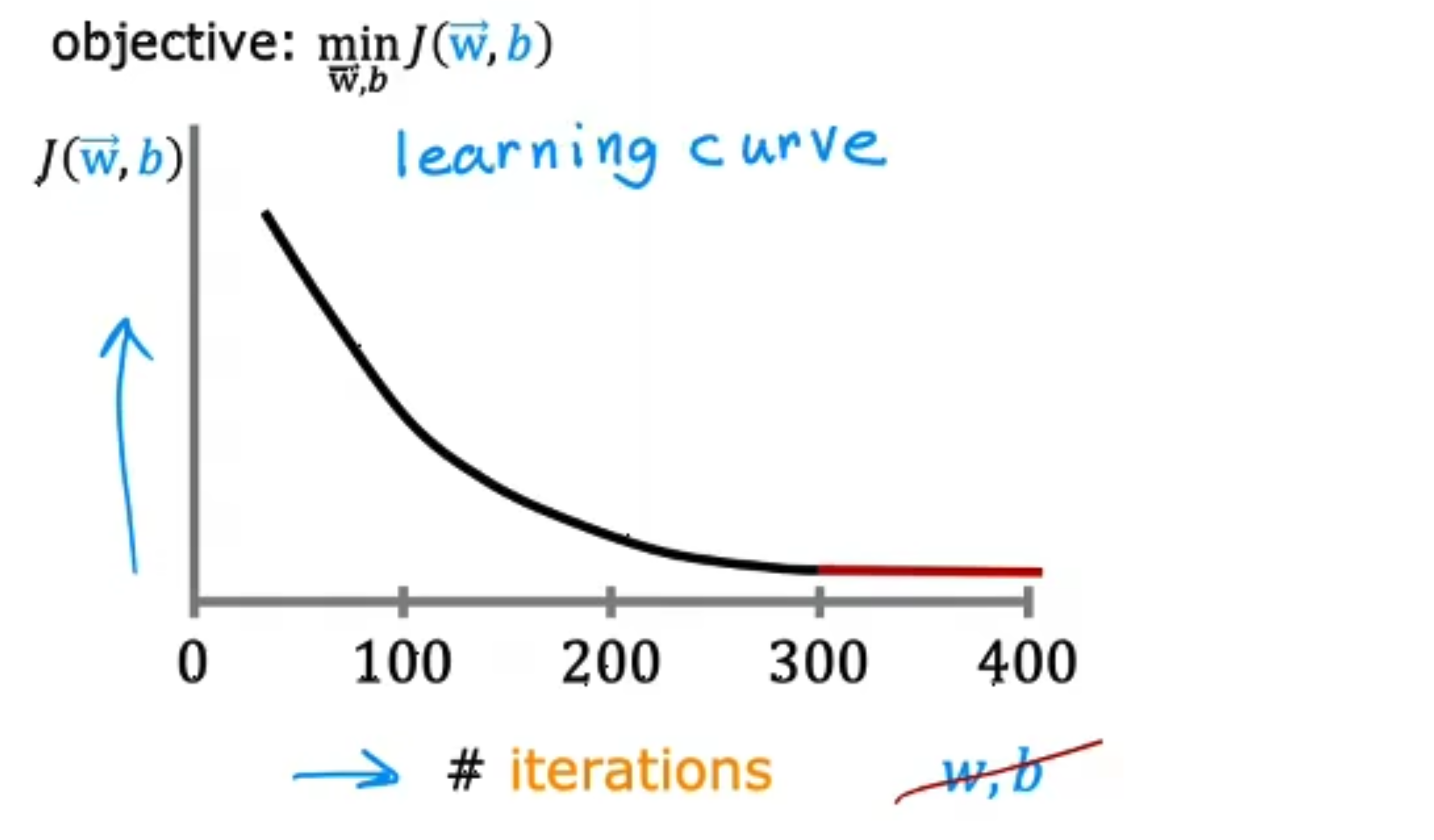
从这个图中可以看到，整个曲线呈一个下降的趋势，如果有一段不下降反而上升了，说明有可能 $\alpha$ 取得太大了，或者程序编写错误了

如果最后的图变得很平缓，说明梯度下降收敛了

我们可以先使用一个较小的 $\alpha$ 来看梯度下降是否收敛，然后慢慢调大，例如，可以从 $0.001$ 开始，每次扩大 10 倍这样子

特征工程

例如我们要估算一个房子的价格，首先我们可以选择房子的长度和宽度作为参数 $x_1,x_2$

这样我们的函数就是 $f(\vec{x})=w_1x_1+w_2x_2+b$

当然，我们同样可以令 $x_3=x_1\times x_2$，于是我们得到的函数可以是 $f(\vec{x})=w_1x_1+w_2x_2+w_3x_3+b$

特征工程指的就是你基于对事物的理解来选取合适的特征

逻辑回归

我们在使用了线性回归之后，还可以使用一个逻辑函数 $g(z)=\frac{1}{1+e^{-z}}$ 来优化回归过程，也就是我们讲的逻辑回归

于是，逻辑回归的柿子就变成了 $$ f(x)=g(z)=\frac{1}{1+e^{-(wx+b)}} $$ 如果我们面临一个二分类问题，即非 $0$ 即 $1$ 那么我们可以设置一个值 $p$ 当预测的参数小于 $p$ 的时候被认为是 $0$，否则被认为是 $1$