底和顶

先给出底和顶的定义

• $\lfloor x \rfloor=$ 小于或者等于 $x$ 的最大整数
• $\lceil x \rceil=$ 大于或者等于 $x$ 的最大整数

我们很容易能得出这两个函数的图像

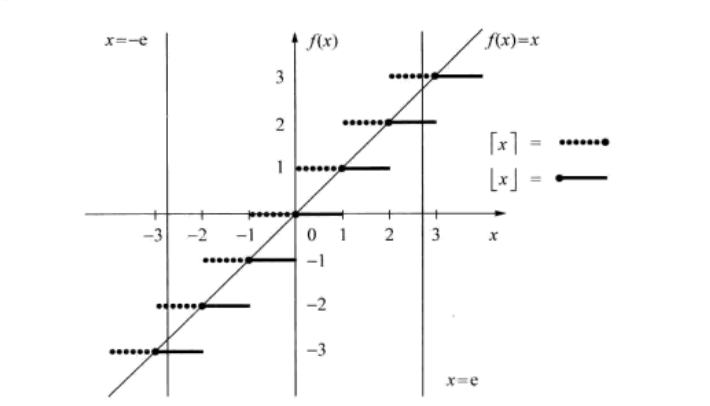
通过这个图像，我们能得出第一个重要不等式：

$x-1<\lfloor x \rfloor \le x \le \lceil x \rceil < x+1$

并且，我们把其中一个函数按照 $x$ 轴对称，然后按照 $y$ 轴对称之后能得到另外一个函数，即：这个是第二个等式

$\lfloor x\rfloor =-\lceil -x\rceil ;\ \lceil x\rceil = -\lfloor -x\rfloor$

根据第一个重要不等式，我们能得出 $x$ 和整数 $n$ 之间的极值不等式关系，这个是第三组不等式

$\begin{aligned} \lfloor x \rfloor &= n \iff n \leq x < n+1, \quad (\text{a}) \\ \lfloor x \rfloor &= n \iff x-1 < n \leq x, \quad (\text{b}) \\ \lceil x \rceil &= n \iff n-1 < x \leq n, \quad (\text{c}) \\ \lceil x \rceil &= n \iff x \leq n < x+1. \quad (\text{d}) \end{aligned}$

我们还有第四组不等式

$\begin{aligned} x < n &\iff \lfloor x \rfloor < n, \quad (\text{a}) \\ n < x &\iff n < \lceil x \rceil, \quad (\text{b}) \\ x \leq n &\iff \lceil x \rceil \leq n, \quad (\text{c}) \\ n \leq x &\iff n \leq \lfloor x \rfloor. \quad (\text{d}) \end{aligned}$

通过这组不等式，就可以做到在一些条件下把底和顶去掉

显然，$\lfloor x \rfloor$ 是 $x$ 的整数部分，那么，我定义 $\{x\}$ 为 $x$ 的分数部分，由此可得 $x=\lfloor x \rfloor + \{x\}$

对于 $\lfloor x+y \rfloor$ 可得，$\lfloor x + y \rfloor=\lfloor x \rfloor +\lfloor y \rfloor+\lfloor \{x\} +\{y\} \rfloor$，又由于 $0\le \{x\}+\{y\} < 2$

那么 $\lfloor x+y \rfloor$ 只有两种情况，要么等于 $\lfloor \{x\} +\{y\} \rfloor$, 要么等于 $\lfloor \{x\} +\{y\} \rfloor+1$