Martian148's blog
martian148
2024-08-29
目录

背包问题

# 背包问题

# 01背包

有 nn 个物品和一个容量为 VV 的背包，每个物品有重量 cic_i 和价值 wiw_i 两种属性，要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总价值不超过背包的容量

定义状态 F[i,v]F[i,v] 表示前 ii 个物品，容量为 vv 的背包所能达到的最大价值

考虑转移，假设当前已经处理好了前 i−1i-1 个物品的状态，那么对于第 ii 个物品，不放入背包时就是 F[i−1,v]F[i-1,v]，放入背包时就是 F[i−1,v−ci]+wiF[i-1,v-c_i]+w_i

转移方程：

F[i,v]=max⁡(F[i−1,v],F[i−1,v−ci]+wi) F[i,v]=\max(F[i-1,v],F[i-1,v-c_i]+w_i)

大部分背包问题的转移方程都是在这个公式上推导出来的，这个方程非常重要，所以详细解释一下：

# 优化空间复杂度

如果直接采用二维数组来进行记录，会出现 MLE。可以改成滚动数组的形式来优化

考虑到对 F[i]F[i] 有影响的只有 F[i−1]F[i-1] ，可以去掉第一维，直接用 F[i]F[i] 来表示处理到当前物品背包容量为 ii 的最大价值，得出以下方程

F[j]=max⁡(F[j],F[j−ci]+wi) F[j]=\max(F[j],F[j-c_i]+w_i)

当我们正着枚举时，发现会发生错误

for (int i = 1; i <= n; i++)
  for (int l = 0; l <= W - w[i]; l++)
    f[l + w[i]] = max(f[l] + v[i], f[l + w[i]]);
1
2
3

对于同一个物品，也就是同一个 ii 中，jj 可能被放入多次，与题意不符

为了避免这种情况的发生，我们可以该边枚举的顺序，从 WW 到 wiw_i，这样 F[i][j]F[i][j] 就会在 F[i][j−wi]F[i][j-w_i] 前先更新，所以更新 F[i][j]F[i][j] 的那个状态就是 F[i−1][j−wi]F[i-1][j-w_i] 与题意相符合

for (int i = 1; i <= n; i++)
  for (int l = W; l >= w[i]; l--) f[l] = max(f[l], f[l - w[i]] + v[i]);
1
2

# 初始化细节问题

事实上，背包有两种不太相同的问法，有些题目要求 ”恰好装满背包“ 时的最优解，有的题目没有要求装满

如果是第一种问法，那么再初始化时除了 F[0]F[0] 为 00 ，其他的 F[1⋯V]F[1\cdots V] 均为 −INF-INF 。这样，F[i]≥0F[i]\ge 0 的 ii 都存在一种方法刚好装到 ii

如果第二种问法，那么初始化时全为 00，这样任何容量的背包都有一个合法解：”什么都不装“

# 一个常数优化

不懂

# 完全背包

完全背包模型与 01 背包类似，与 01 背包的区别仅在于一个物品可以选取无限次，而非仅能选取一次。

我们可以借鉴 01 背包的思路，进行状态定义：设 F[i,v]F[i,v] 为只能选前 ii 个物品时，容量为 vv 的背包可以达到的最大价值。

考虑一种朴素的做法，对于第 ii 件物品，枚举其选了 KK 个来转移。这样的时间复杂度是 O(n3)O(n^3) 的

F[i,v]=max⁡k=0+∞(F[i−1,v−k×ci]+wi×k) F[i,v]=\max\limits_{k=0}^{+\infty}(F[i-1,v-k\times c_i]+w_i\times k)

考虑做一个简单的优化，可以发现对于 F[i,v]F[i,v] ，只要通过 F[i,v−ci]F[i,v-c_i] 来转移就好了

F[i,v]=max⁡(F[i−1,v],F[i,v−ci]+wi) F[i,v]=\max(F[i-1,v],F[i,v-c_i]+w_i)

考虑到在转移时 F[i,v−ci]F[i,v-c_i] 已经被 F[i,v−2×ci]F[i,v-2\times c_i] 更新过，所以 F[i,v−ci]F[i,v-c_i] 就是充分考虑了第 ii 件物品所选次数后得到的最优结果。

我们可以去掉第一维来优化空间复杂度，不难明白压缩后的循环时正向的

for (int i = 1; i <= n; i++)
    for (int l = w[i]; l <= W; l++)
      if (f[l - w[i]] + v[i] > f[l]) f[l] = f[l - w[i]] + v[i];  // 核心状态方程
1
2
3

# 一个简单有效的优化

考虑若两个物品 i,ji,j 满足 ci≤cjc_i \le c_j 且 wi≥wjw_i \ge w_j 则可以将物品 jj 直接去掉，不用考虑。显然，ii 比 jj 更有性价比

具体实现是可以采用 O(n2)O(n^2) 来实现，也可以讲费用大于 VV 的物品去掉，然后使用类似于计数排序的做法，计算出重量相同的物品中，哪个价值最高，是 O(N+V)O(N+V) 的复杂度

对于随机数据能大大减少物品的件数，但是我们可以通过造特殊数据让这种优化失效。

# 多重背包

多重背包也是 01 背包的一个变式。与 01 背包的区别在于每种物品有 kik_i 个，而非一个。

一个很朴素的想法就是：把「每种物品选 kik_i 次」等价转换为「有 kik_i 个相同的物品，每个物品选一次」。这样就转换成了一个 01 背包模型，套用上文所述的方法就可已解决。状态转移方程如下：

F[i,v]=max⁡k=0ki(F[i−1,v−k×ci]+wi×k) F[i,v]=\max\limits_{k=0}^{k_i}(F[i-1,v-k\times c_i]+w_i\times k)

时间复杂度为 O(W∑i=1nki)O(W\sum_{i=1}^{n} k_i)

# 二进制拆分

考虑优化，显然 O(nW)O(nW) 的部分无法优化了，只能从 O(∑ki)O(\sum k_i) 下手

考虑到一种物品有 kik_i 个，而且选择第一个+第二个 和选择 第二个+第三个 完全等价，浪费了很多时间，考虑将一个物品拆分

我们可以通过「二进制分组」的方式

简单的说，就是把 kik_i 拆分成几个 2j2^j 和一个剩余项

例如：

  • 6=1+2+36=1+2+3
  • 8=1+2+4+18=1+2+4+1
  • 18=1+2+4+8+318=1+2+4+8+3

通过这种拆分方式，组合出任意一个 ≤k\le k 的数

时间复杂度 O(W∑i=1nlog⁡2ki)O(W\sum_{i=1}^n \log_2 k_i)

# 混合背包

如果把前面的三种情况混合在一起，也就是说，有的物品可以取一次（01背包），有的物品可以取无限次（完全背包），有的物品可以取的次数有一个上限（多重背包）

# 01 背包与完全背包的混合

考虑在刷 01 背包和完全背包只有第二层遍历顺序的不同，那么我们只需要根据物品的类别选用逆序或者顺序即可，复杂度为 O(nW)O(nW)

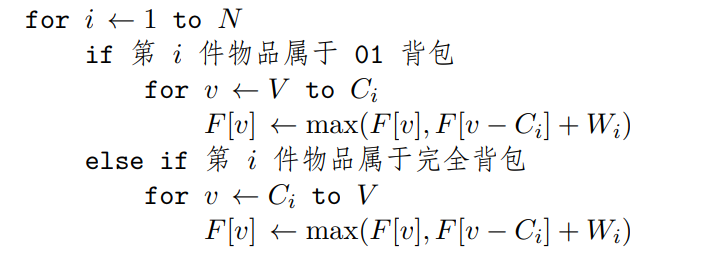
image.png

# 再加上多重背包

我们将一类物品分成 O(log⁡ki)O(\log k_i) 个 01背包

如果考虑单调队列，那么时间复杂度可以优化到 O(nW)O(nW)

最清晰的写法是调用我们前面给出的三个过程。

image.png

# 二维费用的背包问题

二维费用背包只是一个背包有两个费用 cic_i 和 did_i，两种费用可付出的最大值（背包容量）是 VV 和 UU ，物品价值为 wiw_i

方法和 01背包 是类似的，只是多了一维，定义 F[i,v,u]F[i,v,u] 表示枚举到第 ii 个物品，第一个容量装了 vv ，第二个容量装了 uu，转移方程为：

F[i,v,u]=max⁡{F[i−1,v,u],F[i−1,v−ci,u−di]+wi} F[i,v,u]=\max\{F[i-1,v,u],F[i-1,v-c_i,u-d_i]+w_i\}

这个方程也可以采用 01 背包的想法来优化空间

for (int k = 1; k <= ts; k++)          // 循环每一组
  for (int i = m; i >= 0; i--)         // 循环背包容量
    for (int j = 1; j <= cnt[k]; j++)  // 循环该组的每一个物品
      if (i >= w[t[k][j]])             // 背包容量充足
        dp[i] = max(dp[i],
                    dp[i - w[t[k][j]]] + c[t[k][j]]);  // 像0-1背包一样状态转移
1
2
3
4
5
6

这里要注意：一定不能搞错循环顺序，这样才能保证正确性。

# 分组背包

有 NN 个物品和一个容量为 VV 的背包，第 ii 件物品的费用是 cic_i，价值是 wiw_i ，这些物品被划分为 KK 组，每组中的物品互相冲突，最多选一件。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

对于每组来说，要么选一个，要么一个都不选。设 F[k,v]F[k,v] 表示前 kk 组物品花费费用 vv 能取得的最大权值，有

F[k,v]=max⁡{F[k−1,v],F[k−1,v−ci]+wi∣itemi∈groupk⁡} F[k,v]=\max\{F[k-1,v],F[k-1,v-c_i]+w_i\ | \operatorname{item i \in group k} \} 
for (int k = 1; k <= ts; k++)          // 循环每一组
	for (int i = m; i >= 0; i--)         // 循环背包容量
	    for (int j = 1; j <= cnt[k]; j++)  // 循环该组的每一个物品
		    if (i >= w[t[k][j]])             // 背包容量充足
				dp[i] = max(dp[i],dp[i - w[t[k][j]]] + c[t[k][j]]);  // 像0-1背包一样状态转移
1
2
3
4
5

分组的背包问题将彼此互斥的若干物品称为一个组，这建立了一个很好的模型。不少背包问题的变形都可以转化为分组的背包问题。由分组的背包问题进一步可定义“泛化物品”的概念

# 有依赖的背包问题

在背包问题中，可能某些物品之间存在某种 “依赖” 的关系，也就是说，物品 ii 依赖于物品 jj，表示若想选择物品 ii 的先决条件是选了物品 jj。

# 简化的问题

我们先考虑一个比较简单的问题，如果没有某个物品既依赖于别的物品，又被别的物品所依赖。另外，没有某件物品同时依赖多件物品

我们可以把不依赖于别物品的物品称为 "主键"，依赖于某主键的物品称为 “附件”。那么这个简化问题可以看成所有物品由若干主键和依赖于每个主键的一个附件集合组成

考虑一个主键和它的附件集合，可能的方案数达到了 2n+12^n+1 个（主键+每个附件选或者不选）

考虑到所有策略都是互斥的，也就是说，一个主键和他的附件的一种方案可以看成是一个物品，一个主键的所有方案就可以看多是分组背包中的一个物品组。但是这一步转化并不能给出一个好的算法，物品组中的物品还是和原问题的策略一样多

我们想到完全背包那个简单有效的优化，对于第 kk 物品中的物品，对于第 kk 个物品组中的物品，所有费用相同的物品只留一个价值最大的。所以，对主键 kk 的附件集合先进行一次 01背包，得到多件附件重量为 [0⋯V−ck][0\cdots V-c_k] 时的最大价值 F[0⋯V−ck]F[0\cdots V-c_k] 。那么可以把主键以及它的附件集合看成时 V−ck+1V-c_k+1 个物品，其中重量 vv 的物品的价值是 F[V−ck]+wkF[V-c_k]+w_k

然后直接用分组背包的算法解决问题即可

# 较一般的问题

我们去掉那个简化条件，那么依赖关系就是一个图论中的 “森林”。主件的附件可以拥有自己的附件集合，但是附件的附件不能是自己，也就是说，不能产生环

解决这个问题仍然可以用将每个主件及其附件集合转化为物品组的方式。由于附件可能还有附件，我们可以递归的来看，先处理所有儿子节点，把然后再想办法把儿子节点合并，着有点触及到了 “泛化物品” 的思想。

其实数种的每个子树都等价于一个泛化物品，求某节点为根的子树对应的泛化物品相当于求其所有儿子的泛化物品的和

# 泛化物品

考虑这样一种物品，没有固定的重量和价值，物品的价值和你分配给他的重量有关。

在背包容量为 VV 的背包问题种，泛化物品的价值 ww 和重量 cc 之间满足一个函数关系 w=h(c)w=h(c)

在普通的 01背包中，除了给定的 h(c)=wh(c)=w 之外，h(x)h(x) 的所有值都为 00

如果是完全背包，那么 h(c×k)=w×kh(c\times k)=w\times k 其他地方都为 00

如果多重背包，那么每个物品 ii 的 kk 最多到物品的上限 kik_i

显然，在分组背包中的一个组也可以看成是一个泛化物品

# 泛化物品的和

如果给定了两个泛化物品 hh 和 ll，要用一定费用从这两个泛化物品中河道最大价值？也就是要把两个泛化物品合成成一个泛化物品 ff ，我们只需要枚举一个给定的容量 vv ，需要分配多少空间给 hh，多少空间给 ll，也就是

f(v)=max⁡k=0v{h(k)+l(v−k)} f(v)=\max\limits_{k=0}^v\{h(k)+l(v-k)\}

在一个背包问题中，若将两个泛化物品代以它们的和，不影响问题的答案。事实上，对于其中的物品都是泛化物品的背包问题，求它的答案的过程也就是求所有这些泛化物品之和的过程。若问题的和为 ss，则答案就是 s(0⋯V)s(0 \cdots V) 中的最大值。

一个背包问题，无论怎么转化，可能会给出很多条件，包括每种物品的费用、价值等属性，物品之间的分组、依赖等关系等。但肯定能将问题对应于某个泛化物品。

其实可以把泛化物品单纯的理解成一种函数，函数的定义域 0⋯V0\cdots V ，它的值就对于着 vv 大小的背包所对应的最大价值，背包背的过程，就是对多个函数间的合并运算来得到最后的那个总的泛化物品，从总的泛化物品中来得到最后的答案。

这是编程中一种非常常见的抽象思维

# 背包问题变体

传统背包问题要求在背包容量的限制下求可以取到的最大价值，对于一些背包的变体，我们可以修改 FF 数组的定义来得到我们想要的答案

# 输出方案

一般而言，背包问题要求一个最优质，如果要求输出这个最优质的方案，可以参照一般动态规划问题的输出方法：记录下每个状态的最优值是由状态方程的那个策略推出来的。

具体地，方程 F[i,v]=max⁡{F[i−1,v],F[i−1,v−ci]+wi}F[i,v]=\max\{F[i-1,v],F[i-1,v-c_i]+w_i\} ，再用一个数组 G[i,v]G[i,v] 来表示推出 F[i,v]F[i,v] 是用了哪一项，当 G[i,v]=0G[i,v]=0 时表示推出 F[i,v]F[i,v] 的值时时采用了 F[i−1,v]F[i-1,v] ，当 G[i,v]=1G[i,v]=1 时表示采用了 F[i−1,v−ci]F[i-1,v-c_i]

# 输出字典序最小的最优方案

“字典序最小” 指的是 1⋯N1\cdots N 号物品的选择方案排列出来以后字典序最小

# 求方案总数

我们需要得到装满背包或者背包装到一个指定容量的方案数

我们只需要把转移方程中的 max⁡\max 改成 sum{\rm sum} 就好了

F[i,v]=sum{F[i−1,v],F[i−1,v−ci]} F[i,v]={\rm sum} \{F[i-1,v],F[i-1,v-c_i] \}

初始条件时 F[0,0]=1F[0,0]=1

# 最优方案的总数

最优方案是指物品总价值最大的方案，我们结合最大总价值和方案总数，定义 F[i,v]F[i,v] 表示前 ii 个物品，背包大小为 vv 的最大价值，G[i,v]G[i,v] 表示这种状态下的方案数

如果 F[i,v]F[i,v] 是从 F[i−1,v]F[i-1,v] 这里转移过来的，那么 G[i,v]+=G[i−1,v]G[i,v]+=G[i-1,v] ，如果是从 F[i−1,v−ci]F[i-1,v-c_i] 这里转移过来的，那么 G[i,v]+=G[i−1,v−ci]G[i,v]+=G[i-1,v-c_i]

# 回退背包

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll TT = 998244353;
int main() {
    freopen ("F.in", "r", stdin);
    int Q, m; cin >> Q >> m;
    vector<ll> dp (m + 1, 0);
    dp[0] = 1;
    while (Q--) {
        char op; cin >> op;
        int x; cin >> x;
        if (op == '+') {
            for (int i = m; i >= x; i--)
                dp[i] = (dp[i] + dp[i - x]) % TT;
        }
        if (op == '-') {
            for (int i = x; i <= m; i++)
                dp[i] = (dp[i] - dp[i - x] + TT) % TT;
        }
        cout << dp[m] << '\n';
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
上次更新: 2024/11/06, 21:08:59
半平面交
DP优化

← DP优化→

最近更新
01
逻辑学
12-13
02
中华传统文化
12-12
03
欧拉回路
11-14
更多文章>
Theme by Vdoing | Copyright © 2024-2024 Martian148 | MIT License