珂朵莉树

# 珂朵莉树

# 什么是珂朵莉树

珂朵莉树，又称Old Driver Tree(ODT)~~（老司机树）~~。

是一种基于 std::set 的暴力数据结构。

# 什么时候用珂朵莉树

使一整段区间内的东西变得一样，数据随机。

以下以 CF896C 为板子来介绍珂朵莉树。

$n$ 个数， $m$ 次操作 $(n,m \le 10^5)$

操作：

区间加
区间赋值
区间第k小
求区间幂次和

数据随机，时限2s。

# 核心思想

把值相同的区间合并成一个结点保存在 $set$ 里面。

# 实现

# 珂朵莉树的初始化

这道题里，这样定义珂朵莉树的节点：

struct node
{
    int l,r; //范围
    mutable LL v; //数值
    node(int L, int R=-1, LL V=0):l(L), r(R), v(V) {}
    bool operator<(const node& o) const     //重载运算符
    {
        return l < o.l;
    }
};

1
2
3
4
5
6
7
8
9
10

表示 $[l,r]$ 这一个区间中所有的数都是v。

mutable 的意思是「可变的」，让我们可以在后面的操作中修改 v 的值。在 C++ 中，mutable 是为了突破 const 的限制而设置的。被 mutable 修饰的变量（mutable 只能用于修饰类中的非静态数据成员），将永远处于可变的状态，即使在一个 const 函数中。

这意味着，我们可以直接修改已经插入 set 的元素的 v 值，而不用将该元素取出后重新加入 set

# 珂朵莉树的核心操作拆分：split

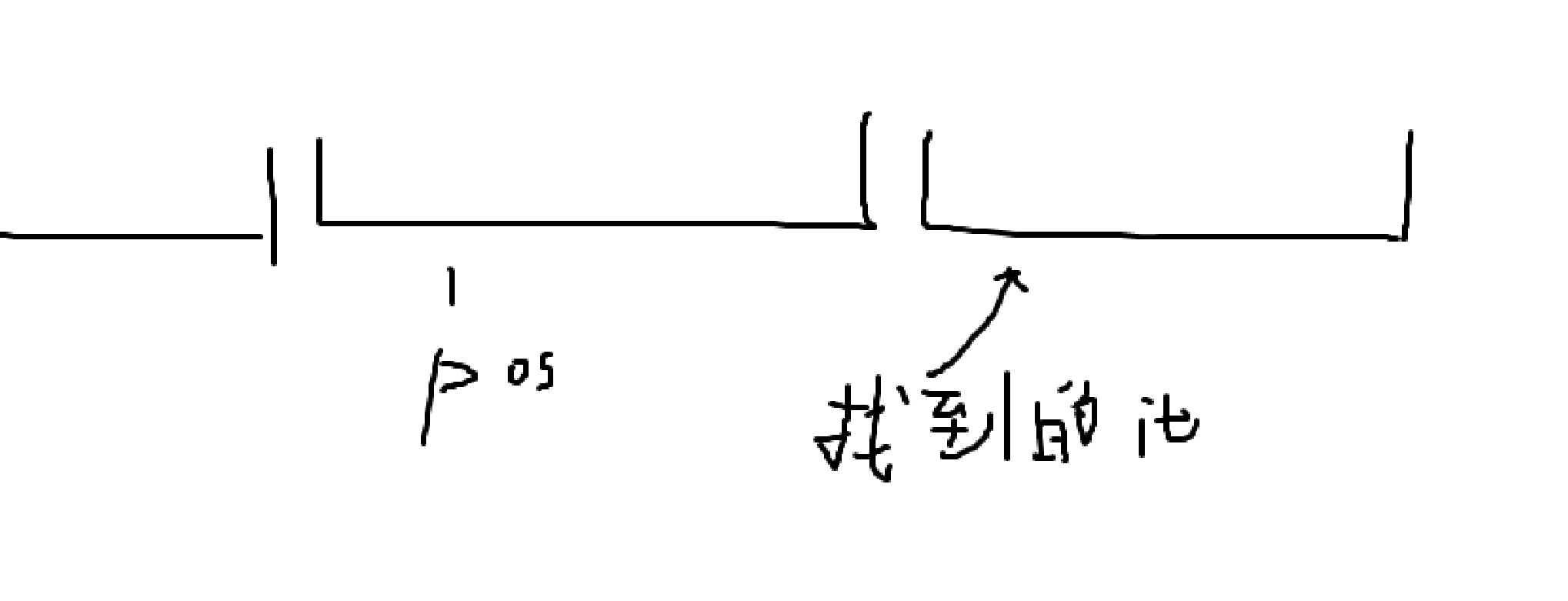
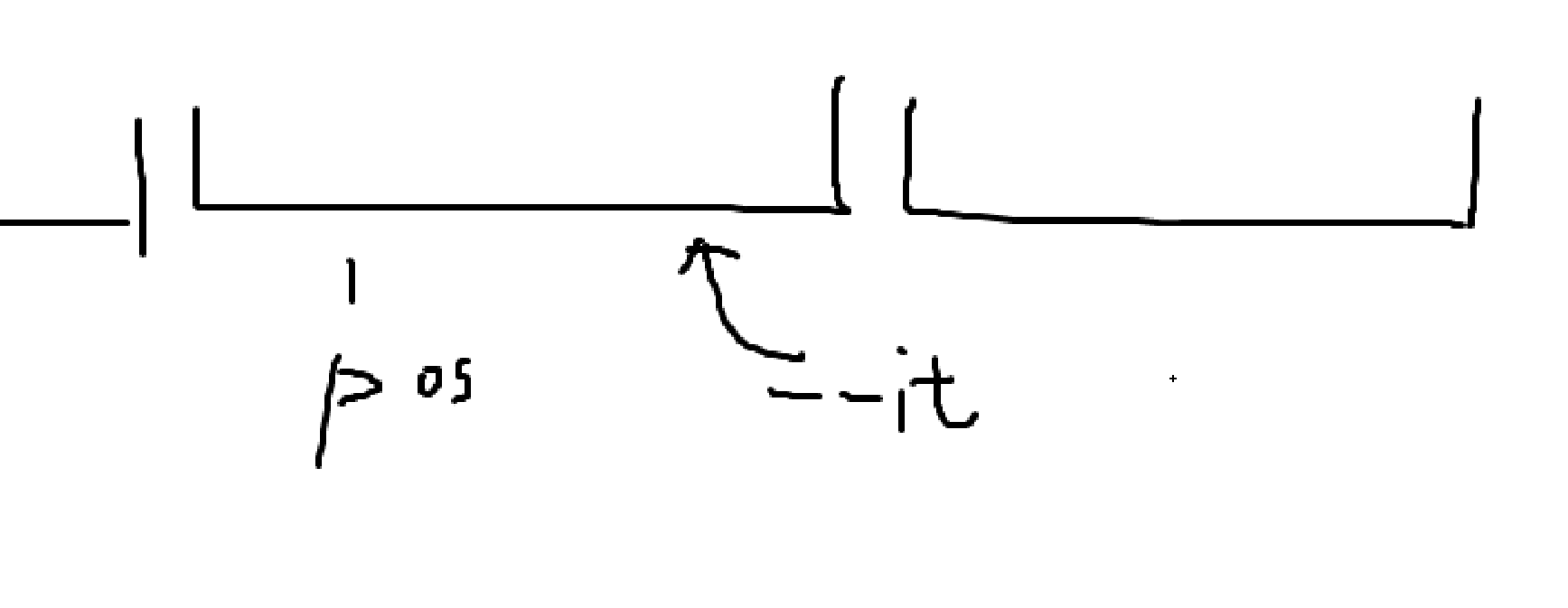
实际很简单，一个集合中，有一部分需要修改，而另一部分不需要修改，就把集合拆开，拆成两部分，把原来包含 $x$ 的区间 $[l,r]$ 分裂成 $[l,x)$ 和 $[x,r]$ 并且返回指向后者的迭代器

#define IT set<node>::iterator  //太长了 迭代器

IT split(int pos)
{
    IT it = s.lower_bound(node(pos));   //找到首个左端点不小于pos的set
    if (it != s.end() && it->l == pos)   //如果开头就是x无需分裂，直接返回
        return it;
    --it;  //否则一定在前一个区间中
    int L = it->l, R = it->r;  //【l,r】就是要分裂的区间
    LL V = it->v;  //取出值
    s.erase(it);   //删除原集合
    s.insert(node(L, pos-1, V));  //构建前半段的新结合
    return s.insert(node(pos, R, V)).first;  //构建后半段的新集合并且返回迭代器
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 珂朵莉树的推平操作：assign_val

要是只有split还不得复杂度爆炸？我们需要assign操作迅速减少set的数量。

void assign_val(int l, int r, LL val)
{
    IT itr = split(r+1),itl = split(l);  //求出要被摊平区间的收尾地址
    s.erase(itl, itr);  //删除原集合
    s.insert(node(l, r, val));  //添加新集合
}

1
2
3
4
5
6

需要注意一个细节，split(r+1)要在spilt(l)之前

珂朵莉树的复杂度是由assign_val保证的。

由于数据随机，有1/4的操作为assign。

set 的大小快速下降，最终趋于 logn ，使得这种看似暴力无比的数据结构复杂度接近mlogn

# 其他操作（一个比一个暴力）

1.区间加

void add(int l, int r, LL val)
{
    IT itr = split(r+1), itl = split(l);
    for (; itl != itr; ++itl) 
        itl->v += val;
}

1
2
3
4
5
6

反正就是找到对应集合暴力一加（有点像分块）

2.区间第k小

LL rank(int l, int r, int k)
{
    vector<pair<LL, int> > vp;
    IT itr = split(r+1),itl = split(l);
    vp.clear();
    for (; itl != itr; ++itl)
        vp.push_back(pair<LL,int>(itl->v, itl->r - itl->l + 1));  // 第一个元素是值，第二个元素是长度
    sort(vp.begin(), vp.end());
    for (vector<pair<LL,int> >::iterator it=vp.begin();it!=vp.end();++it)
    {
        k -= it->second;
        if (k <= 0) 
            return it->first;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

把元素取出，暴力排序，暴力查找第k小，结束

3.区间幂次和

LL pown(LL a, LL b, LL mod)
{
    LL res = 1;
    LL ans = a % mod;
    while (b)
    {
        if (b&1) 
            res = res * ans % mod;
        ans = ans * ans % mod;
        b>>=1;
    }
    return res;
}

LL sum(int l, int r, int ex, int mod)
{
    IT itr = split(r+1), itl = split(l);
    LL res = 0;
    for (; itl != itr; ++itl)
        res = (res + (LL)(itl->r - itl->l + 1) * pown(itl->v, LL(ex), LL(mod))) % mod;
    return res;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

暴力找到元素，快速幂，加入答案，结束（记得不要忘乘上集合里的个数）！！！

没什么可说的

上代码

#include<bits/stdc++.h>
#define IT set<node>::iterator
using namespace std;
typedef long long LL;
const int MOD7 = 1e9 + 7;
const int MOD9 = 1e9 + 9;
const int imax_n = 1e5 + 7;
struct node
{
    int l,r;
    mutable LL v;
    node(int L, int R=-1, LL V=0):l(L), r(R), v(V) {}
    bool operator<(const node& o) const
    {
        return l < o.l;
    }
};
LL pown(LL a, LL b, LL mod)
{
    LL res = 1;
    LL ans = a % mod;
    while (b)
    {
        if (b&1) 
            res = res * ans % mod;
        ans = ans * ans % mod;
        b>>=1;
    }
    return res;
}
set<node> s;
IT split(int pos)
{
    IT it = s.lower_bound(node(pos));
    if (it != s.end() && it->l == pos) 
        return it;
    --it;
    int L = it->l, R = it->r;
    LL V = it->v;
    s.erase(it);
    s.insert(node(L, pos-1, V));
    return s.insert(node(pos, R, V)).first;
}
void add(int l, int r, LL val)
{
    IT itr = split(r+1),itl = split(l);
    for (; itl != itr; ++itl) 
        itl->v += val;
}
void assign_val(int l, int r, LL val)
{
    IT itr = split(r+1),itl = split(l);
    s.erase(itl, itr);
    s.insert(node(l, r, val));
}
LL ranks(int l, int r, int k)
{
    vector<pair<LL, int> > vp;
    IT itr = split(r+1),itl = split(l);
    vp.clear();
    for (; itl != itr; ++itl)
        vp.push_back(pair<LL,int>(itl->v, itl->r - itl->l + 1));
    sort(vp.begin(), vp.end());
    for (vector<pair<LL,int> >::iterator it=vp.begin();it!=vp.end();++it)
    {
        k -= it->second;
        if (k <= 0) 
            return it->first;
    }
}
LL sum(int l, int r, int ex, int mod)
{
    IT itr = split(r+1),itl = split(l);
    LL res = 0;
    for (; itl != itr; ++itl)
        res = (res + (LL)(itl->r - itl->l + 1) * pown(itl->v, LL(ex), LL(mod))) % mod;
    return res;
}
int n, m;
LL seed, vmax;
LL rd()
{
    LL ret = seed;
    seed = (seed * 7 + 13) % MOD7;
    return ret;
}
LL a[imax_n];
int main()
{
    cin>>n>>m>>seed>>vmax;
    for (int i=1; i<=n; ++i)
    {
        a[i] = (rd() % vmax) + 1;
        s.insert(node(i,i,a[i]));
    }
    s.insert(node(n+1, n+1, 0));
    int lines = 0;
    for (int i =1; i <= m; ++i)
    {
        int op = int(rd() % 4) + 1;
        int l = int(rd() % n) + 1;
        int r = int(rd() % n) + 1;
        if (l > r)
            swap(l,r);
        int x, y;
        if (op == 3)
            x = int(rd() % (r-l+1)) + 1;
        else
            x = int(rd() % vmax) +1;
        if (op == 4)
            y = int(rd() % vmax) + 1;
        if (op == 1)
            add(l, r, LL(x));
        else if (op == 2)
            assign_val(l, r, LL(x));
        else if (op == 3)
            cout<<ranks(l,r,x)<<endl;
        else
            cout<<sum(l,r,x,y)<<endl;
    }
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122

上次更新: 2025/04/08, 18:03:31

← 笛卡尔树数论→