 Codeforces Round 969 (Div. 2) A-D 题解
Codeforces Round 969 (Div. 2) A-D 题解
# Codeforces Round 969 (Div. 2)
Codeforces Round 969 (Div. 2) (opens new window)
# A - Dora's Set
# Question
集合 包含 内的所有整数,每次能选择三个整数 满足:,就能从集合中删去 ,问最多能进行几次删除操作
# Solution
考虑 ,如果 是一个奇数,并且 ,则能一次删除
所以只需要模拟删除过程就好了
# Code
#include <bits/stdc++.h>
using namespace std;
int main() {
freopen ("A.in", "r", stdin);
int T; cin >> T;
while (T--) {
int l, r; cin >> l >> r;
if (l % 2 == 0) l += 1;
if (r % 2 == 1) r += 1;
int len = r - l + 1;
cout << len / 4 << '\n';
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
# B - Index and Maximum Value
# Question
在她的生日派对上收到了另一个整数数组 后,Index 决定对它进行一些操作。
具体来说,她将按顺序执行 个操作,每个操作属于以下两种类型之一:
- 。 给定两个整数 和 ,对于所有 ,满足 ,将 。
- 。 给定两个整数 和 ,对于所有 ,满足 ,将 。
Index 对数组 中的最大值感到好奇。请帮助她在执行每个操作后找到最大值。
# Solution
如果此次的最大值为 ,如果 没有操作,那么最大值必然不会大于 ,如果 操作了,那么最大值必然是 ,所以,其实只需要维护原数列中的最大值来做所有操作就好了
# Code
#include <bits/stdc++.h>
using namespace std;
int main() {
freopen ("B.in", "r", stdin);
int T; cin >> T;
while (T--) {
int n, m; cin >> n >> m;
vector<int> a(n);
for (int i = 0; i < n; i++) cin >> a[i];
int m_ = *max_element(a.begin(), a.end());
while (m--) {
char op; cin >> op;
int l, r; cin >> l >> r;
if (op == '+' && l <= m_ && m_ <= r) m_ += 1;
else if (op == '-' && l <= m_ && m_ <= r) m_ -= 1;
cout << m_ << ' ';
}
cout << '\n';
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# C - Dora and C++
# Question
给定一个序列,可以给单点 或 ,求多次操作后的极差
# Solution
根据裴蜀定理,,可以转化成 ,所以考虑对于每个数在 的定义下考虑这个问题
对序列排序去重后的序列为 ,枚举最小值 ,那么最大值就是 ,极差就是
# Code
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
int main() {
freopen ("C.in", "r", stdin);
ios::sync_with_stdio(0); cin.tie(0);
int T; cin >> T;
while (T--) {
int n, a, b; cin >> n >> a >> b;
int g = __gcd(a, b);
vector<int> c(n + 1);
for (int i = 1; i <= n; i++) cin >> c[i];
for (int i = 1; i <= n; i++) c[i] = c[i] % g;
auto c_ = c;
sort(c_.begin() + 1, c_.end());
c_.erase(unique(c_.begin() + 1, c_.end()), c_.end());
int m = c_.size() - 1;
int ans = INF;
for (int i = 1; i <= m; i++) {
int pre = (i == 1) ? m : i - 1;
int now = (c_[pre] - c_[i] + g) % g;
ans = min(ans, now);
}
cout << ans << '\n';
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# D - Iris and Game on Tree
# Question
Iris 有一棵以 为根的树。每个顶点都有一个值为 或 。
我们考虑树的一个叶子节点(顶点 永远不会被考虑为叶子节点),并定义它的权值。构造一个字符串,由从根开始到这个叶子节点的路径上的顶点的值组成。那么该叶子节点的权值是它中包含 和 子串数量之差。
以下面这棵树为例。绿色的顶点值为 ,白色的顶点值为 。
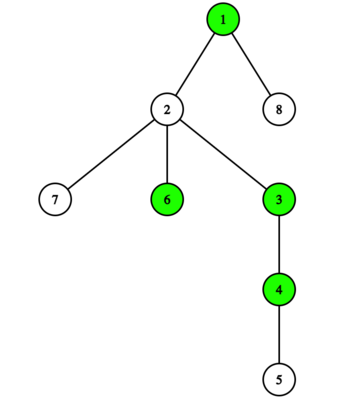
- 计算叶子节点 的权值:构造出的字符串为 。其中, 的出现次数为 , 的出现次数为 ,所以它们的数量之差为 。
- 计算叶子节点 的权值:构造出的字符串为 。其中, 的出现次数为 , 的出现次数为 ,所以它们的数量之差为 。
树的得分定义为树中权值不为零的叶子节点数。
但是,一些顶点的值尚未确定,将以 给出。填充这些空白区域很无聊,所以 Iris 打算邀请 Dora 玩一个游戏。每一轮,两个女孩中的一个可以选择任何剩余值为 的顶点,并将其值更改为 或 ,Iris 先手。游戏将一直进行,直到树中没有值为 的顶点为止。Iris 的目标是最大化树的得分,而 Dora 的目标是最小化它。
假设两个女孩都采取最优策略,请确定树的最终得分。
# Solution
先考虑什么字符串能让树的得分增加,手玩几组就会发现 01 子串和 10 子串数量不同,等价于第一个和第二个字母是否相同,对应到图中就是根节点的权值和叶子节点的权值
如果根节点的权值已经确定了,那么他们肯定优先去修改叶子节点
如果根节点的权值是 ?,那么就要分类讨论了
- 如果叶子节点 的个数多,那么根节点选
- 如果叶子节点 的个数多,那么根节点选
- 如果叶子节点 数量一样多,那么先手去修改根节点的人比吃亏,所以去取非根非叶子节点,非根非叶子节点取完后再取根节点,所以谁先手去修改根节点取决于非根非叶子节点的奇偶性
# Code
#include <bits/stdc++.h>
using namespace std;
int main() {
freopen ("D.in", "r", stdin);
int T; cin >> T;
while (T--) {
int n; cin >> n;
vector<int> du(n + 1, 0);
vector<vector<int>> g(n + 1);
int ans = 0;
int cnt_leaf = 0, cnt_other = 0;
int leaf_0 = 0, leaf_1 = 0;
for (int i = 1; i < n; i++) {
int u, v; cin >> u >> v;
du[u] += 1, du[v] += 1;
g[u].push_back(v); g[v].push_back(u);
}
string s; cin >> s; s = " " + s;
for (int i = 1; i <= n; i++) {
if (i == 1) continue;
if (du[i] == 1) {
if (s[i] == '?') cnt_leaf += 1;
if (s[i] == '0') leaf_0 += 1;
if (s[i] == '1') leaf_1 += 1;
}
else {
if (s[i] == '?') cnt_other += 1;
}
}
int cnt = cnt_leaf + cnt_other + (s[1] == '?');
if (s[1] == '?') {
if (leaf_0 > leaf_1) {
ans += leaf_0;
ans += cnt_leaf / 2;
}
else if (leaf_0 < leaf_1) {
ans += leaf_1;
ans += cnt_leaf / 2;
}
else {
if (cnt_other % 2 == 0) {
ans += cnt_leaf / 2;
ans += leaf_0;
}
else {
ans += (cnt_leaf + 1) / 2;
ans += leaf_0;
}
}
}
else {
if (s[1] == '0')
ans += leaf_1;
else
ans += leaf_0;
ans += (cnt_leaf + 1) / 2;
}
cout << ans << '\n';
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
