在知乎上看到一种记忆六个三角函数很好的方法，记录一下

六边形记忆法

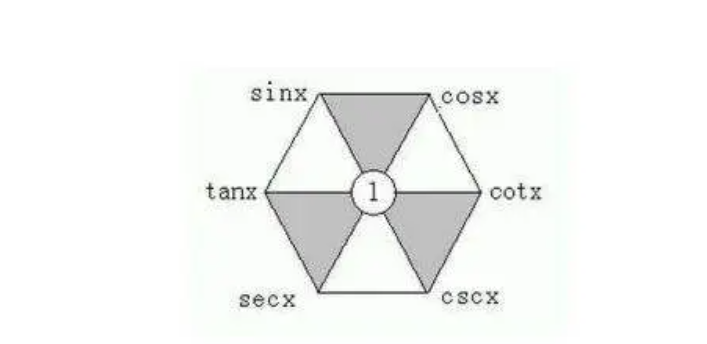
纵向的来看，左半都为 "正"，右半都为 “余”

横向的来看，最上面一行为 “弦”，中间一行为 “切”，最后一行为 “割”

对角线都是互为倒数的关系

我们注意到六边形的中间有一个 $1$ ，和杨辉三角很像，一个倒三角形内，上面的两个元素的平方和等于下面那个元素的平方和，也就是

$\begin{aligned} \sin ^2 x+\cos ^2 x =1\\ \tan ^2 x+ 1 =\sec ^2 x\\ 1 +\cot ^2 x =\csc ^2 x \end{aligned}$

六边形每个顶点都等于与它相邻的两个函数的乘积，比如 $\sec x =\tan x \times \csc x$