线性代数

矩阵乘法

$c_{ij}=\sum_{k=1}^n a_{ik}b_{kj}$

我们定义了乘法，那么我们就可以用使用快速幂来实现矩阵运算

常见的递推形式

1. $f(n)=a_1f(n-1)+a_2f(n-2)+\cdots+a_kf(n-k)$

$\begin{pmatrix} f(n) \\ f(n-1)\\ f(n-2)\\ \vdots\\f(n-k+1) \end{pmatrix} =\begin{pmatrix} a_1 &a_2 &\cdots &a_k \\ 1 & 0 & \cdots & 0\\ 0& 1& \cdots &0\\ \vdots& & \ddots &\vdots\\0 & \cdots & 1 & 0 \end{pmatrix} \begin{pmatrix} f(n-1) \\ f(n-2)\\ f(n-3)\\ \vdots\\f(n-k) \end{pmatrix}$

2. $f(n)=a_1f(n-1)+a_2f(n-2)+C$

$\begin{pmatrix} f(n) \\ f(n-1)\\1 \end{pmatrix} =\begin{pmatrix} a_1 &a_2 &C \\ 1 & 0 & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} f(n-1) \\ f(n-2)\\1 \end{pmatrix}$

当然，这种形式很容易推到到有 $k$ 项的形式

3. $f(n)=a_1f(n-1)+a_2f(n-2)+c_2n^2+c_1n+c_0$

$\begin{pmatrix} f(n) \\ f(n-1)\\(n+1)^2\\n+1\\1 \end{pmatrix} =\begin{pmatrix} a_1 &a_2 &C_2&C_1&C_0 \\ 1&0&0&0&0\\ 0&0&1&2&1\\ 0&0&0&1&1\\ 0&0&0&0&1 \end{pmatrix} \begin{pmatrix} f(n-1) \\ f(n-2)\\n^2\\n\\1 \end{pmatrix}$

4. $f(n)=a_{11}f(n-1)+a_{12},g(n)=a_{21}f(n-1)+a_{22}g(n-1)$

$\begin{pmatrix} f(n) \\ g(n) \end{pmatrix} =\begin{pmatrix} a_{11}&a_{12}\\ a_{21}&a_{22} \end{pmatrix} \begin{pmatrix} f(n-1) \\ g(n-1) \end{pmatrix}$

这个是两个函数相互有关系，但这些关系都是线性的

• 可以把矩阵运算看成和数值的运算类似，可以用线段树等数据结构维护

• 动态DP

高斯消元

一个线性方程组有 $m$ 个一次方程，$n$ 个变量，把所有的系数写成一个 $m$ 行 $n$ 列的矩阵，把每个方程等号右侧的常

数放在最右列，得到一个 $m$ 行 $n+1$ 列的增广矩阵

高斯消元通过多次变换把方程组转化为多个一元一次方程

高斯消元具体步骤：

• 枚举每一列，找到第一个

线性方程组的解有 $3$ 种情况，有唯一解，有无穷多解，无解

高斯-约当消元法

高斯-约旦消元法的前提是 （假设有唯一解）

消元过程如下

1. 从第 $1$ 列开始，选择一个非 $0$ 的系数（一般是最大值）所在的行，把这一行与第一行交换，此时 $x_1$ 是主元
2. 把 $x_1$ 的系数转换成 1
3. 利用主元 $x_1$ 的系数，把其他行的这一列的主元消去
4. 重复以上步数，直到把每行都变成只有对角线上存在主元，且系数都为 $1$，则答案就是最后一列的数字

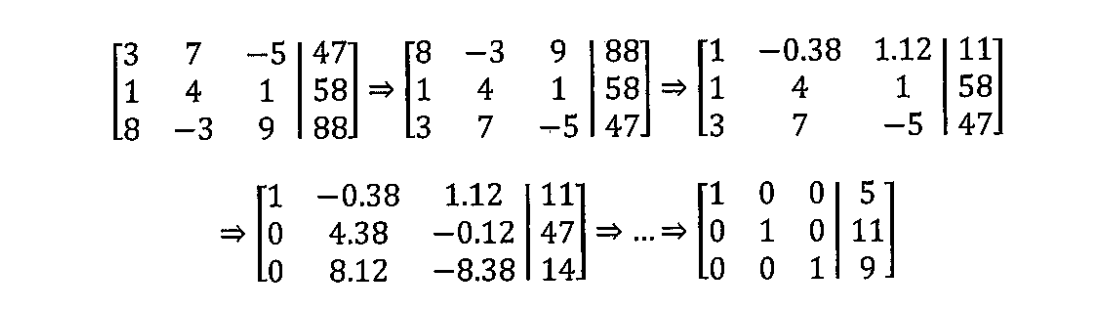
std::string gauss(std::vector<std::vector<ld>> &a) { // 传入增广矩阵
    int n = a.size();
    int c = 0, r = 0;
    for (c = 0, r = 0, c < n; c ++) {
        int tmp = r;
        for (int i = r; i < n; i++)
            if (sgn(a[i][c]))
                tmp = i;
        if (sgn(a[tmp][c]) == 0)
            continue;

        std::swap(a[tmp], a[r]);

        for (int i = n; i >= c; i--)
            a[r][i] /= a[r][c];
        
        for (int i = r + 1; i < n; i++)
            if (sgn(a[i][c]))
                for (int j = n; j >= c; j--)
                    a[i][j] -= a[r][j] * a[i][c];
        r += 1;
    }
    if (r < n) {
        for (int i = r; i < n; i++)
            if (sgn(a[i][n]))
                return "NoSolution";
        return "InfSolution";
    }

    for (int i = n - 1; i >= 0; i--)
        for (int j = i + 1; j < n; j++)
            a[i][n] -= a[j][n] * a[i][j];
    
    return "OK";
}

线性基

基是线性代数中的一个概念，一个向量空间可以由一组基线性组合而成

而线性基指的是模 $2$ 域中的基

我们可以把这样一种线性的思想带到异或中去来组成线性基

线性基解决以下几类问题

从 $n$ 个数中选出任意个数，使得异或和最大

一种朴素的思想是 $2^n$ 次暴力枚举，但是由于每个数特别小，可能有多个组合能异或成为一个数，所以我们理论上来说答案只有 $2^m$ 种，$m$ 为最大的二进制位数

线性基的构造

1. 非高斯消元构造

考虑到如果每个数的二进制位数都不同，那么这个集合 $A$ 的线性基就是它本身

如果有两个数的二进制位数相同，那么通过 $a_1 \oplus a_2$ 可以把最高位去掉，所以我们枚举每个数去匹配位数，如果这一位有数了，那么就把当前枚举的这个数来异或上这个位的数，以此来消去枚举的这一个数的这一位上的一

2. 高斯消元构造线性基

利用高斯消元来构造线性基会更加直观

把原数组构成的矩阵进行高斯消元，化成简化阶梯矩阵

如果后面有全 $0$ 项，说明原来的集合 ${A}$ 中存在一种方案使得异或和为 $0$

线性基的应用

最小异或和

只需要判断是否有 $0$ 存在即可

最大异或和

若用基本方法求线性基，对于最后求出的基 $P$ ，从大到小尝试异或每个元素，如果异或这个元素使得答案变大的话，那就异或它

如果用高斯消元的方法求线性基，由于只有对角线上存在 $1$ ，那么把 $P$ 中所有数字异或起来就是答案

第 $k$ 大/小异或和

高斯消元后，第 $k$ 小异或和就是选上 $k$ 二进制分解后为 $1$ 的那些行

//带求第 k 大的板子
struct Linear_basis {
    i64 num[70]{}, zero = 0;
    const int B = 62;
    bool insert(i64 x) {
        for (int i = B; i >= 0; i --) if (x & (1ll << i)) {
            if (num[i]) x ^= num[i];
            else {
                num[i] = x;
                return true;
            }
        }
        zero ++;
        return false;
    }

    i64 query_min(i64 x) {
        for (int i = B; i >= 0; i --)
            x = std::min(x, x ^ num[i]);
        return x;
    }

    i64 query_max(i64 x) {
        for (int i = B; i >= 0; i --)
            x = std::max(x, x ^ num[i]);
        return x;
    }

    i64 query_kth(i64 k) {
        i64 x = 0;
        k >>= zero;
        std::vector<i64> p;
        for (int i = 0; i <= B; i ++) if (num[i]) p.emplace_back(num[i]);
        for (int i = (int)p.size() - 1; i >= 0; i --) {
            if (k & (1ll << i)) x = std::max(x, x ^ p[i]);
            else x = std::min(x, x ^ p[i]);
        }
        return x;
    }
} lb;