KMP

KMP 主要是处理这一类问题

给定一个文本串 $S$ 和一个模式串 $P$，在 $S$ 中找出 $P$ 第一次出现的位置

暴力匹配算法

暴力很好想，从 $S$ 的第一个字符开始，逐个与 $P$ 的字符进行比较，如果匹配成功，则继续比较下一个字符，否则从 $S$ 的下一个字符开始重新比较

int match(string s, string p) // 串匹配算法
{
    int lens = s.length(); // 文本串长度
    int lenp = p.length(); // 模式串长度
    int i = 0, j = 0;      // i指向文本串，j指向模式串，代表当前比对字符的位置
    while (i < lens && j < lenp)
    {
        if (s[i] == p[j]) // 若匹配
        {
            i++;
            j++; // 同时后移，跳转至下一个字符
        }
        else // 若不匹配
        {
            i -= j - 1; // 文本串回退
            j = 0;      // 模式串复位
        }
    }
    return i - j; // 返回匹配位置
}

int match(string s,string p) {
    int lens = s.length(), lenp = p.length(), i = 0, j = 0;
    for (i = 0; i < lens - lenp + 1; i++){
        for (j = 0; j < lenp; j++)
            if (p[i + j] != s[j])
                break;
        if(j >= lenp)
            break; //找到匹配子串
    }
    return i;
}

暴力的时间复杂度是 $O(nm)$，$n,m$ 分别为串的长度

KMP算法

构思

观察一种特殊的情况，可以让暴力的时间复杂度为 $O(nm)$

S: 000000000……0000001
P: 0001

我们发现，造成复杂度太大的原因是因为大量的局部匹配，每一轮的 $m$ 次对比中，仅最后一次可能失配。一旦发现失配，文本串，模式串的字符的指针都要回退，并从头开始下一轮的尝试

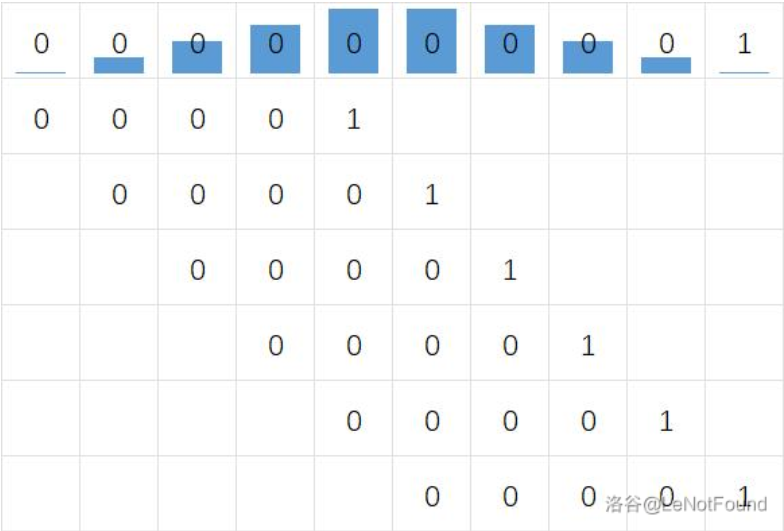
只要局部匹配很多，效率必将很低

实际上，重复的对比操作没有必要，既然我们已经掌握了 $S$ 中的 $[i-j.j)$ 的全部信息，也就是说它具体是由那些字符所构成的，而这类信息，完全可以为后续的各部对比所利用

回到刚才那个例子，观察一次迭代中失败的那次对比，尽管这次对比是失败的，但意味着，我们在此之前已经获得了足够多次成功的匹配，在这个例子中，也就是 $0-0$ 匹配，也就是说，在主串中所对于的子串，完全是由 $0$ 构成的。之前的暴力算法没有注意到并且充分利用这一点，如果将这个特性利用起来，我们就可以每次大幅度地向右滑动，从而降低复杂度

.. |0|0 0 0 0 0|0 0 0 ...
   |0|0 0 0 0 0|1
   | |0 0 0 0 0|0 1

对于如上情况，我们可以发现，即便下一轮迭代只能将模式串整体右移一个字符，但相较于暴力算法，中间那五个连续的 $0$，也就是第三行中模式串的 $[0,5)$ 这个前缀，都不用再继续比对了，我们只需要从竖线右边开始对比即可

如此一来，$i$ 将完全不必回退！现在我们想的一个流程：

• 比对成功，则与 $j$ 同步前进一个字符
• 否则，$j$ 更新为某个更小的 $t$ ，并继续比对

再一个更为复杂的情况，考察如下的文本串和模式串

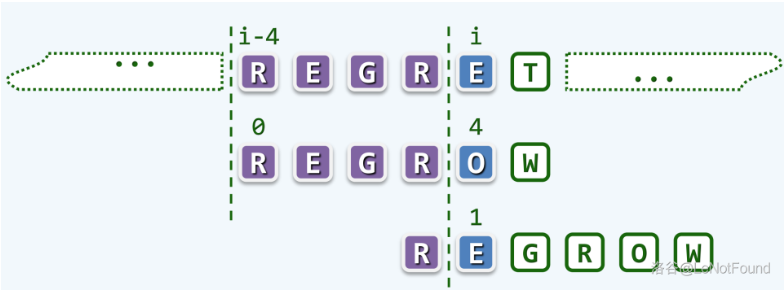
这一轮的迭代，首次失配于 $E$ 和 $O$ 的失配，这里并不需要一步一步的右移模式串，可以大胆地将其后移 $3$ 个字符

next 表

一般地，如果前一轮对比终止于 $S[i] \ne P[j]$。 $i$ 指针不必回退，而是 $S[i]$ 与 $P[t]$ 对齐并开始下一轮对比。那么 $t$ 应该取什么值呢？

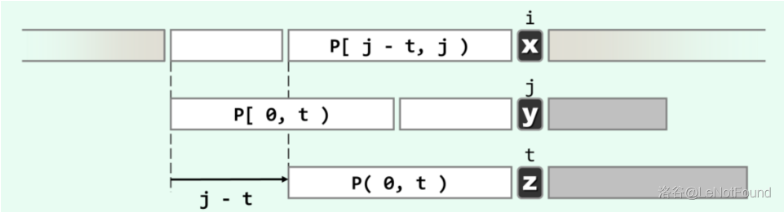
由图可见，经过此前一轮的比对，已经可以确定匹配的范围应为：

$P[0,j)=S[i-j,i)$

于是，若模式串 $P$ 经适当右移之后，能够与 $S$ 的某一 （包括 $S[i]$ 在内的）子串完全匹配，必要条件就是

$P[0,t)=S[i-t,i)=P[j-t,j)$

通过上面这个式子表示了，$P[0,j)$ 中 长度为 $t$ 的真前缀，应与长度为 $t$ 的真后缀完全匹配，故 $t$ 必来自集合 ：

$N(P,j=0\le t< j)\ |\ P[0,t)=P[j-t,j)$

这个式子表示了，$t$ 仅取决于模式串 $P$ ，和文本串 $S$ 无关！

显然，一个集合中可能包含多个这样的 $t$，那么应该取那个作为 $next[j]$ 呢？

从图中可以看出下一轮的对比从 $S[i]$ 和 $P[t]$ 开始，这等效于将 $P$ 右移了 $j-t$ 个单元，位移量与 $t$ 成反比。因此，为保证不遗漏任何可能的匹配，应该在 $N(P,j)$ 中选择最大的 $t$ ，也就是说，当有多个值得试探的右移方案时，应该保守地选择其中移动距离最短者。于是，若令

$next[j]=\max(N(P,j))$

一旦发现 $P[j]$ 与 $S[i]$ 失配，即可转而将 $P[next[j]]$ 与 $S[i]$ 对齐，开始下一轮对比

既然集合 $N(P,j)$ 与文本串无关，所以对于任一模式串 $P$，可以通过预处理提前处理计算出所有位置 $j$ 所对于的 $next[j]$

实现

int match(string s,string p) {
    vector<int> nxt = build_next(p);
    int len_s = s.length(),len_p = p.length();
    int i = 0,j = 0;
    while(j < len_p && i < len_s) {
        if (0 > j || s[i] == p[j]) // 若匹配，或 p 已移出最左侧（两个判断的次序不可交换）
            i += 1, j += 1;
        else
            j= nxt[j];
    }
    return i - j;
}

提示：若使用万能头且声明形如 vector<int> next 的数组，则数组名称不能使用 next，会与 stl_iterator_base_funcs.h 中的保留关键字 next 冲突.

构造next表

• $\text{next}[0] = -1$

不难看出，只要 $j>0$ 则必有 $0 \in N(P,j)$ 。此时 $N(P,j)$ 非空，从而可以保证 "在其中取最大值" 这一操作可行，但反过来，若 $j=0$ ，则即便 $N(P,j)$ 可以定义，也必是空集

那么 $next[0]$ 怎么定义呢？$next[0]$ 的调用条件是第一次匹配就失败，我们应该把 $P$ 串向右移动一个单位，然后启动下次比较，由于下一次比较时 $i++,j++$，我们可以把 $next[0]$ 定义为 $-1$ ，就可以让 $S[i+1]$ 和 $P[0]$ 进行匹配了

• $next[j+1]$

那么，已知 $next[0,j]$，如何才能快速的递推出 $next[j+1]$ 呢？

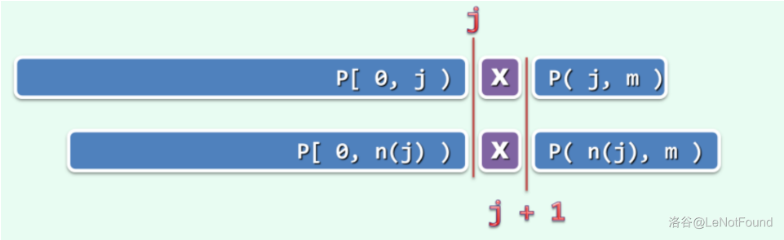
若 $\text{next}[j]=t$，意味着在 $P[0,j)$ 中，自匹配的真前缀和真后缀的最大长度为 $t$ ，则必有 $next[j+1] \le next[j]+1$，当且仅当 $P[j]=P[t]$ 时如上图取等号

如何理解？

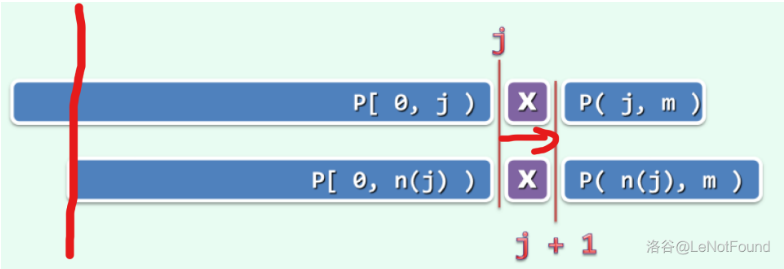
以左边的红线为界，可以发现，下面的 $P$ 的前缀，与上面的子串是完全匹配的，如果 $P[j+1]=P[next[j]+1]=X$ 那么发现上面的从红线开始到 $j+1$ 和下面的从红线开始到 $P[next[j]+1]$ 都是匹配的，而这正是 $next[j+1]$ 的定义

所以一般地，若 $P[j] \ne P[t]$ 又怎么办呢？

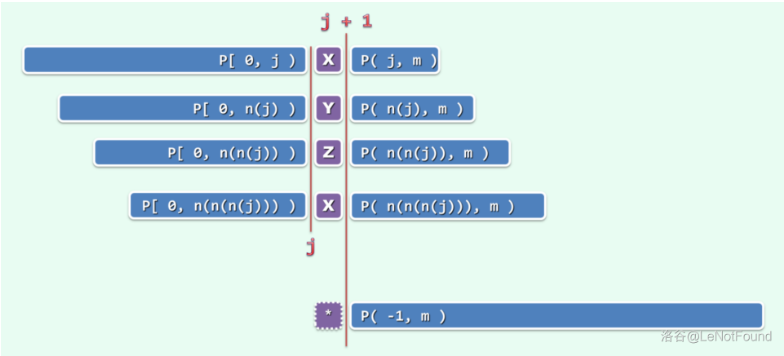
有点类似于 $S$ 串和 $P$ 串的匹配，这里可以可以看成是 $P$ 串 与 $P$ 串的匹配，如果 $P[j+1]$ 与 $P[next[j]+1]$ 失配了，就换下一个 $next[]$ 即，$P[j+1]$ 与 $P[next[next[j]]]+1]$ 匹配，以此类推

由于 $next[t]<t$ 所以如果不能匹配， $t$ 必然会降至 $0$，然后使用上面定义的 $next[0]=-1$ 来进行下一次匹配

vector<int> build_next(string p){
    int len_p=p.length(),j=0;
    vector<int> nxt(len_p);
    int t=nxt[0]=-1;
    while(j<len_p-1){
        if(0>t||p[j]==p[t])
            j++,t++,nxt[j]=t;
        else
            t=nxt[t];
    }
    return nxt;
}

洛谷 P3375 (opens new window)

#include <bits/stdc++.h>
using namespace std;

vector<int> build_next(string p) {
    int len = p.size(), j = 0;
    vector<int> nxt(len + 1, 0);
    int t = nxt[0] = -1;
    while (j < len) {
        if (0 > t || p[j] == p[t])
            j += 1, t += 1, nxt[j] = t;
        else 
            t = nxt[t];
    }
    return nxt;
}

vector<int> kmp(string s, string p) {
    auto nxt = build_next(p);
    vector<int> ans;
    int i = 0, j = 0;
    while (i < s.size() && j < int(p.size())) {
        if (0 > j || s[i] == p[j]) {
            i += 1, j += 1;
            if (j == p.size()) {
                ans.push_back(i - j + 1);
                j = nxt[j];
            }
        }
        else
            j = nxt[j];
    }
    return ans;
}

int main() {
    string s, p; cin >> s >> p;
    auto ans = kmp(s, p);
    for (auto x : ans)
        cout << x << "\n";
    vector<int> nxt = build_next(p);
    for (int i = 1; i < nxt.size(); i++)
        cout << nxt[i] << " ";
    cout << '\n';
    return 0;
}