堆

左偏树

左偏树是一种非常常见且好写的可并堆

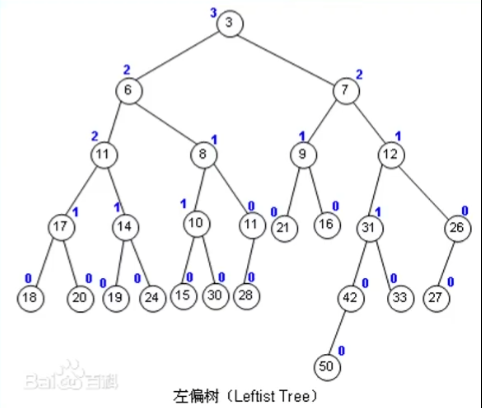
圆圈内部是结点的键值，首先满足堆的性质，所以键值肯定小于等于其儿子结点的键值（小根堆）

蓝色数字就是我们定义的一个距离 dist，定义为结点到外节点的距离，其中外界点为儿子数量小于 $2$ 的节点，外界点的 dist 为 $0$

左偏树保证 左儿子的 dist $\ge$ 右儿子的 dist

所以，很容易可以推出，一个节点的 dist $=$ 右儿子的 dist $+1$

特别的空节点的距离为 $-1$

一个 $n$ 个节点的左偏树根节点的 $dist \le \log(n+1)-1$

定义节点

struct Node {
	int val, dist, rs, ls;
	Node() {val = rs = ls = 0;dist = -1;}
	Node(int val) : val(val), dist(0), rs(0), ls(0) {}
};

合并

合并操作是左偏树操作中最繁琐的一个，但它有点像 LCT 的 Access 操作

在合并过程中，我们需要维护好左偏树的性质，具体过程如下，我们设需要合并的两个堆的根节点记做 $x,y$ 且 $val_x\le val_y$

• 根据堆的性质，所以合并完之后的根还是 $x$，递归合并 $y$ 和 $x$ 的右儿子
• 由于合并完成之后可能破坏 $x$ 的左偏性质，如果违反了则交换左右儿子
• 然后更新 $x$ 的 $dist$ ，为右儿子 $+1$

int merge (int x, int y) {
	if (x == 0 || y == 0) return x | y; // 如果有一个是空的，就返回另一个
	if (t[x].val > t[y].val) swap(x, y); // 保证x是较小的
	t[x].rs = merge(t[x].rs, y); // 将x的右儿子和y合并
	if (t[t[x].ls].dist < t[t[x].rs].dist) swap(t[x].ls, t[x].rs); // 保证左儿子的dist大于右儿子
	t[x].dist = t[t[x].rs].dist + 1; // 更新dist
	t[t[x].rs].fa = t[t[x].ls].fa = x;
	return x; // 返回合并后的根节点
}

插入节点

把单个节点看作一个堆，合并即可

删除根

合并根的左右儿子

整个堆加上/乘上一个值

和平衡树上打标记类似，堆上也可以打上标记，然后在遍历到的时候 pushdown 即可

删除某个节点

需要多维护一个节点的父亲

先合并这个节点的左右节点，然后更新这个节点的祖先节点

void push_up(int x) {
	if (!x) return ;
	if (t[x].dist != t[t[x].rs].dist + 1) {
		t[x].dist = t[t[x].rs].dist + 1;
		push_up(t[x].fa);
	}
}

void erase(int x) {
	int y = merge(t[x].ls, t[x].rs);
	t[y].fa = t[x].fa;
	if (t[t[x].fa].ls == x) t[t[x].fa].ls = y;
	else if (t[t[x].fa].rs == x) t[t[x].fa].rs = y;
	push_up(t[x].fa);
}