 平衡树
平衡树
# 平衡树
# 替罪羊树
在所有能维护二叉树平衡的 BST 中,最简单的是替罪羊树:如果发现树上有一棵子树不平衡了,那就摧毁它(先中序遍历出子树上所有元素,再删除整棵子树),然后以中间元素为根,重新建立一棵平衡的子树

与其他 BST 对比,替罪羊树调整平衡的方法没有任何技巧,但是替罪羊树依然有着检索,插入,删除的平坦复杂度为
替罪羊树的计算复杂度和维护二叉平衡树的效果取决于设定的不平衡率 alpha
我们怎么样才能判定一个二叉平衡树是 “不平衡的”,不可能只要不是对称的就认为是不平衡的
于是,我们定义一颗以 为根的子树,如果它的左子树和右子树占比大于 alpha,就认为不平衡,alpha ,alpha 越大,树越不平衡,极端的,alpha 二叉树是绝对平衡的,表现为一棵满二叉树
设定一个 alpha 值,用暴力维持二叉树的不平衡率在 alpha 内,这就是替罪羊树的思想
# 基本操作
# 定义
struct Node{
int lson,rson;
int val,siz,tsiz,fa; //子树大小。真实子树大小
int real; //真实
Node(){
lson=rson=0;
val=siz=tsiz=fa=0;
real=1;
}
};
2
3
4
5
6
7
8
9
10
# 删除
先讲删除是因为替罪羊树的删除和别的 BST 不一样,他的删除是假性删除
因为删除的左右节点很难处理,就是在节点上打上一个删除标记,标记它名存实亡了,然后在重构的时候再忽略它
当一个子树已经被删除的节点达到一定数量时,例如子树的 那么就可以重构子树了
# 代码实现
#include<bits/stdc++.h>
using namespace std;
struct Node{
int lson,rson;
int val,siz,tsiz,fa; //子树大小。正式子树大小
int real; //真实
Node(){
lson=rson=0;
val=siz=tsiz=fa=0;
real=1;
}
};
struct BST{
vector<Node> t;
vector<int> order;
const double aplpha=0.75; //平衡因子
int root=0,tot=0,rb=0;
BST(int n){
t.assign(1,Node());
}
bool nobalance(int u){ //判断平衡
if((double)t[u].tsiz*aplpha < (double)max(t[t[u].lson].tsiz,t[t[u].rson].tsiz)) return true;
return false;
}
void insert(int& u,int val){
if(!u){
t.push_back(Node());
u=++tot;
t[u].val=val;
t[u].siz=t[u].tsiz=t[u].real=1;
t[u].lson=t[u].rson=0;
return ;
}
t[u].siz++;t[u].tsiz++;
if(val<=t[u].val) insert(t[u].lson,val);
else insert(t[u].rson,val);
if(isbad(u)) rebuild(u);
}
int kth(int k){
for(int u=root;u;){
if(t[u].real&&t[t[u].lson].tsiz+1==k)
return t[u].val;
if(t[t[u].lson].tsiz>=k)
u=t[u].lson;
else
k-=t[t[u].lson].tsiz+t[u].real,
u=t[u].rson;
}
return 0;
}
int rank(int val){ //返回值 val 的排名
int ans=1;
for(int u=root;u;){
if(val<=t[u].val)
u=t[u].lson;
else
ans+=t[t[u].lson].tsiz+t[u].real,
u=t[u].rson;
}
return ans;
}
void pop_rk(int &u,int rk){ //删除排名为 rk 的节点
if(t[u].real&&t[t[u].lson].tsiz+1==rk){ //找到了
t[u].real=0;
t[u].tsiz--;
return ;
}
t[u].tsiz--;
if(t[t[u].lson].tsiz+t[u].real>=rk) //在左子树
pop_rk(t[u].lson,rk);
else
pop_rk(t[u].rson,rk-(t[t[u].lson].tsiz+t[u].real));
}
void pop(int val){ //删除值为 val 的节点
pop_rk(root,rank(val)); //先找到排名
if(1.0*t[root].siz*aplpha > 1.0*t[root].tsiz) //如果无用节点过多,重建
rebuild(root);
}
void dfs(int u){
if(!u) return ;
dfs(t[u].lson);
if(t[u].real) order.push_back(u);
dfs(t[u].rson);
}
void build(int &u,int l,int r,int fa=0){
int mid=(l+r)>>1;
u=order[mid];
t[u].fa=fa;
if(l==r){
t[u].lson=t[u].rson=0;
t[u].siz=t[u].tsiz=1;
return ;
}
if(l<mid)
build(t[u].lson,l,mid-1,u);
else
t[u].lson=0;
if(r>mid)
build(t[u].rson,mid+1,r,u);
else
t[u].rson=0;
t[u].siz=t[t[u].lson].siz+t[t[u].rson].siz+1;
t[u].tsiz=t[t[u].lson].tsiz+t[t[u].rson].tsiz+t[u].real;
}
void rebuild(int &u){
order.assign(1,0);
dfs(u);
if(order.size()!=1) //没有新的元素
build(u,1,order.size()-1,t[u].fa);
else
u=0;
}
};
int main(){
freopen("P3369.in","r",stdin);
freopen("P3369.out","w",stdout);
int Q; scanf("%d",&Q);
BST T(Q);
int op,x;
while(Q--){
scanf("%d%d",&op,&x);
if(op==1){
T.insert(T.root,x);
// if(T.rb) { //重建
// if(T.rb==T.root) T.rebuild(T.root);
// else if(T.rb==T.t[T.t[T.rb].fa].lson) T.rebuild(T.t[T.t[T.rb].fa].lson);
// else T.rebuild(T.t[T.t[T.rb].fa].rson);
// T.rb=0;
// }
}
if(op==2){
T.pop(x);
}
if(op==3){
printf("%d\n",T.rank(x));
}
if(op==4){
printf("%d\n",T.kth(x));
}
if(op==5){
printf("%d\n",T.kth(T.rank(x)-1));
}
if(op==6){
printf("%d\n",T.kth(T.rank(x+1)));
}
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
# Splay 树
Treap 树解决平衡的办法是给每个节点加上一个随机的优先级,实现概率上的平衡。但实际上不需要额外加一个优先级,而是观察树的形态,发现不平衡就直接调整成平衡态
Splay 树的基本操作是把某个节点通过旋转提升为根节点。分裂:先把 旋转到根,然后分为两棵树 和 , 上节点的键值小于 上节点的键值。合并:把 的最小节点 旋转到根,此时 的左儿子为空,然后把 挂到 的左儿子上
FHQ Treap 树和 Splay 树的区别:
- 有些场合必须使用 Splay 树,如动态树 LCT,因为 LCT 的复杂度证明要用 Splay 树证明的势能法
- FHQ Treap 树能做可持久化,而 Splay 树不适合做持久化。可持久化的关键是用较小的空间储存相邻时间点的两棵树的变化,避免空间爆炸。FHQ Treap 是 "无旋" 的,相邻时间点的两棵树的形态差异较小。而 Splay 树的基本操作是旋转,导致相邻时间点的两棵树差异很大
# 定义节点
struct Node {
int fa, ch[2], siz, val;
};
2
3
# 旋转
那么,如何设计把一个节点 旋转到根的方法,需要达到以下两个目的
- 每次旋转,节点 就上升一层
- 旋转改善 的平衡性,即尽量使二叉树层次变少,从根到叶子节点的路径变短,平均的层数和路径长度为
如果只考虑目的 (1) 那么使用 Treap 树的旋转法即可,这种旋转被称为 “单旋”,单旋不会减少二叉树的层数,Splay 树主要使用双旋,即两次单旋,同时旋转 个节点,,父亲 ,祖父 。双旋分为两种:一字旋,之字旋。我们记左旋为 ,右旋为
单旋,做一次 或 。此时, 在距离根只有 层的位置,只需要做一次单旋即可
一字旋。此时 在一条线上,做双旋 或 。若 是 的左儿子, 是 的左儿子,做两次 ,反之做两次 。注意,应该先旋转 和 再旋转
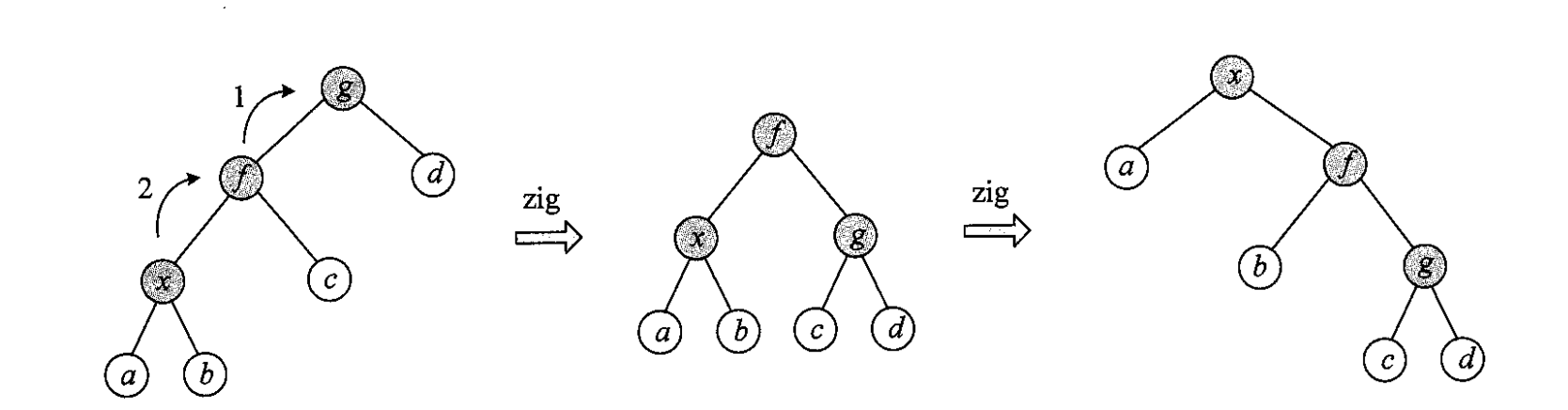
- 之字旋。此时 不在一条线上,做双旋 或 ,若 是 的左儿子, 是 的右儿子,做 否则做 注意要先旋转 和 ,再旋转 和 ,之字旋也能减少二叉树的层数
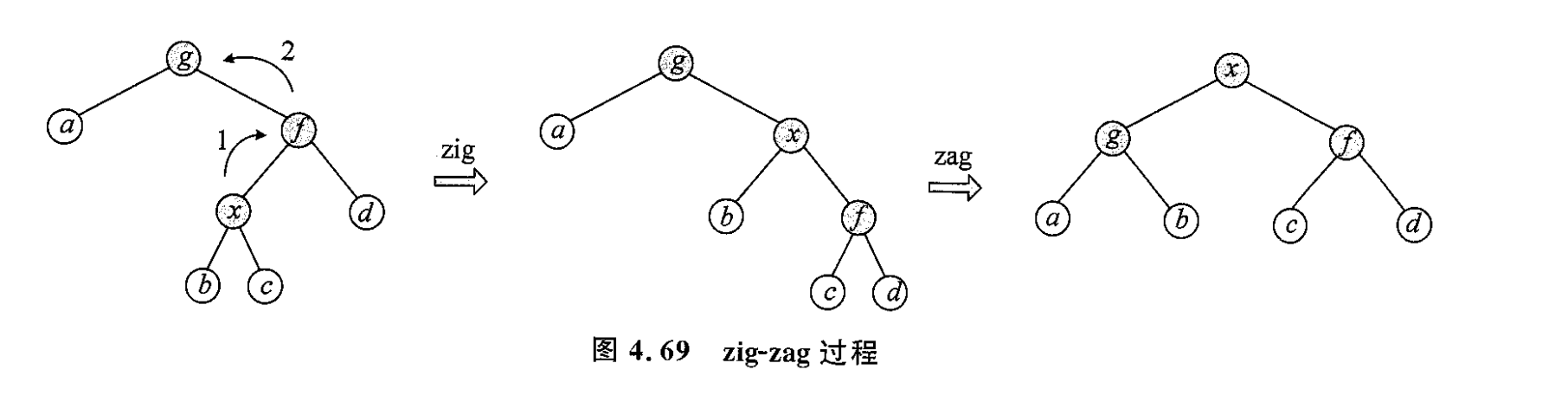
在具体实现的时候,代码的写法可能有所不同,我们先定义两个辅助函数 和
bool ident(int x,int f) 用于判断 是 的左儿子还是右儿子,如果左儿子就返回 ,右儿子返回
bool ident (int x, int f) {return t[f].ch[1] == x;}
connect(int x, int f, int op) 用于把 和 建立父子关系,把 作为 的儿子, 就是左儿子, 就是右儿子
void connect (int x, int f, int s){ //把 x 连接到 f 的 s 侧
t[f].ch[s] = x;
t[x].fa = f;
}
2
3
4
我们把伸展操作分成两个函数实现 ,rotate (int x) 和 splay(int x, int top)
rotate(int x) 用于把 往上旋一个单位,定义 是 的父亲节点。也就是说,如果 是 的左儿子,那么就对 右旋,如果 是 的右儿子,那么就对 左旋
再定义 为 的父亲,也就是 的祖父, 表示 是 的左子树还是右子树
旋转分为三步
- 连接 和其祖父 ,也就是提
- 把 之后需要连 的那个儿子给
- 把 连到 的儿子节点
最后更新 和
void rotate (int x){
int f = t[x].fa, g = t[f].fa, k = ident(x,f);
connect(x,g,ident(f,g)); connect(t[x].ch[k^1],f,k); connect(f,x,k^1);
push_up(f); push_up(x); // push_up 用于更新一些信息
}
2
3
4
5
splay(int x,int top) 函数用于把 转到 的儿子节点, 时则把 转到根节点
还是一样,定义 为 的父亲, 为 的父亲
如果 说明之需要一次单旋就好了,也就是把 向上提一层
否则就是双旋,如果 说明是一字形,减少先转 再转 ,否则就是先转 再转
还有要注意的一点就是记得更新
void splay (int x, int top) { //代表把x转到top的儿子,top为0则转到根结点
if (top == 0) root = x;
while (t[x].fa != top) {
int f = t[x].fa, g = t[f].fa;
if (g != top) {
if (ident(x, f) == ident(f, g)) rotate(f);
else rotate(x);
}
rotate(x);
}
}
2
3
4
5
6
7
8
9
10
11
# 插入
首先需要定义函数 newnode(int &x,int f,int val),用于新建一个节点
void newnode(int &x,int f,int val){
t[x=++cnt].fa = f; t[x].val=val; t[x].siz=1;
}
2
3
插入新的节点就是需要找到插入位置,然后新建节点,最后把这个节点 到根节点
void insert(int val, int &x = rt, int fa = 0){
if(!x)
newnode(x,fa,val), splay(x,0);
else if(val < t[x].val)
insert(val,t[x].ch[0],x);
else
insert(val,t[x].ch[1],x);
}
2
3
4
5
6
7
8
# 删除
删除节点分为两步,第一步是找到这个节点,第二步是删除这个节点
找到这个节点非常简单,关键在于如何删除
void del(int val,int x = rt){
if(val == t[x].val)
delnode(x);
else if(val < t[x].val)
del(val,t[x].ch[0]);
else
del(val,t[x].ch[1]);
}
2
3
4
5
6
7
8
假设需要删除的节点为 ,我们先把 节点移到根节点,如果这个节点没有右儿子,那么直接把根赋值为 的左儿子,相当于删除了 。如果 有右儿子,找到 的后继 ,把 伸展到 的右儿子处,此时 肯定是没有左儿子的,那么就把 的左儿子作为 的左儿子,把根节点赋值为 ,就相当于删去了
void del_node(int x) { // 注意这里可能存在内存浪费
splay(x, 0);
if (t[x].ch[1]) { // 存在右节点
int p = t[x].ch[1]; // 找 x 的后继节点
while (t[p].ch[0]) p = t[p].ch[0];
splay(p, x);
connect(t[x].ch[0], p, 0);
root = p; t[root].fa = 0;
push_up(p);
}
else {
root = t[x].ch[0];
t[root].fa = 0;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 排名
get_rank(int val) 用于查找 在 Splay 中的排名
从根节点开始往下走,去寻找 的位置,累计答案
- 如果 说明在左节点
- 如果 说明在右节点, 加上左儿子的大小和根节点的大小
找到后把 伸展到根节点
int get_rank(int val) {
int x = root, res = 1, pre = 0;
while (x) {
if (val <= t[x].val) x = t[x].ch[0], pre = x;
else res += t[t[x].ch[0]].siz + 1, x = t[x].ch[1];
}
if (pre) splay(pre, 0);
return res;
}
2
3
4
5
6
7
8
9
# 第 大值
查找第 大值,从根出发,
- 如果左子树大小 说明就是这个节点
- 如果左子树的大小 ,说明在左子树
- 否则在右子树,此时需要更新 值, 值减去左子树大小
int kth(int k){
int x = rt;
while(x){
if(k == t[t[x].ch[0]].siz + 1){
splay(x,0); break;
}
else if(k <= t[t[x].ch[0]].siz)
x = t[x].ch[0];
else
k -= t[t[x].ch[0]].siz + 1, x = t[x].ch[1];
}
return t[x].val;
}
2
3
4
5
6
7
8
9
10
11
12
13
# 找前驱节点
int pre(int val, int x) {
if (!x) return -INF;
if (val <= t[x].val) return pre(val, t[x].ch[0]);
else return max(t[x].val, pre(val, t[x].ch[1]));
}
2
3
4
5
# 后继节点
int nxt(int val, int x) {
if (!x) return INF;
if (val >= t[x].val) return nxt(val, t[x].ch[1]);
else return min(t[x].val, nxt(val, t[x].ch[0]));
}
2
3
4
5
# 例题
// splay
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
struct Node {
int fa, ch[2], siz, val;
};
struct Splay {
vector<Node> t;
int root, tot;
Splay(int n) {
root = tot = 0;
t.resize(n);
}
bool ident(int x, int f) {return t[f].ch[1] == x;}
void connect (int x, int f, int s) {
t[f].ch[s] = x;
t[x].fa = f;
}
void push_up (int x) {
t[x].siz = t[t[x].ch[0]].siz + t[t[x].ch[1]].siz + 1;
}
void rotate (int x) {
int f = t[x].fa, g = t[f].fa, k = ident(x, f);
connect(x, g, ident(f, g));
connect(t[x].ch[k ^ 1], f, k);
connect(f, x, k ^ 1);
push_up(f); push_up(x);
}
void splay (int x, int top) { //代表把x转到top的儿子,top为0则转到根结点
if (top == 0) root = x;
while (t[x].fa != top) {
int f = t[x].fa, g = t[f].fa;
if (g != top) {
if (ident(x, f) == ident(f, g)) rotate(f);
else rotate(x);
}
rotate(x);
}
}
void new_node (int &x, int f, int val) {
x = ++tot;
t[x].fa = f;
t[x].val = val;
t[x].siz = 1;
t[x].ch[0] = t[x].ch[1] = 0;
}
void insert (int val, int &x, int f) {
if (!x) new_node(x, f, val), splay(x, 0);
else {
if (val < t[x].val) insert(val, t[x].ch[0], x);
else insert(val, t[x].ch[1], x);
}
}
void del_node(int x) { // 注意这里可能存在内存浪费
splay(x, 0);
if (t[x].ch[1]) { // 存在右节点
int p = t[x].ch[1]; // 找 x 的后继节点
while (t[p].ch[0]) p = t[p].ch[0];
splay(p, x);
connect(t[x].ch[0], p, 0);
root = p; t[root].fa = 0;
push_up(p);
}
else {
root = t[x].ch[0];
t[root].fa = 0;
}
}
void del(int val, int x) {
if (val == t[x].val) del_node(x);
else {
if (val < t[x].val) del(val, t[x].ch[0]);
else del(val, t[x].ch[1]);
}
}
int get_rank(int val) {
int x = root, res = 1, pre = 0;
while (x) {
if (val <= t[x].val) x = t[x].ch[0], pre = x;
else res += t[t[x].ch[0]].siz + 1, x = t[x].ch[1];
}
if (pre) splay(pre, 0);
return res;
}
int kth(int k) {
int x = root;
while (x) {
if (k == t[t[x].ch[0]].siz + 1) {
splay(x, 0); break;
}
else {
if (k <= t[t[x].ch[0]].siz) x = t[x].ch[0];
else k -= t[t[x].ch[0]].siz + 1, x = t[x].ch[1];
}
}
return t[x].val;
}
int pre(int val, int x) {
if (!x) return -INF;
if (val <= t[x].val) return pre(val, t[x].ch[0]);
else return max(t[x].val, pre(val, t[x].ch[1]));
}
int nxt(int val, int x) {
if (!x) return INF;
if (val >= t[x].val) return nxt(val, t[x].ch[1]);
else return min(t[x].val, nxt(val, t[x].ch[0]));
}
};
Splay t(100005);
int main() {
ios::sync_with_stdio(false);
int T; cin >> T;
while (T--) {
int op, x; cin >> op >> x;
if (op == 1) t.insert(x, t.root, 0);
else if (op == 2) t.del(x, t.root);
else if (op == 3) cout << t.get_rank(x)<< endl;
else if (op == 4) cout << t.kth(x) << endl;
else if (op == 5) cout << t.pre(x, t.root) << endl;
else if (op == 6) cout << t.nxt(x, t.root) << endl;
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
# Treap 树
Treap 是一个合成词,把 Tree 和 Heap 各取一半组合而成,因此 Treap 是树和堆的结合
每个节点有一个键值和一个优先级,对于键值,这颗树是一个 BST,对于优先级这个树是一个大根堆
若我们每次给一个节点一个随机的优先级,那么从期望概率上来说就实现了 BST 的平衡,插入删除查找的时间复杂度都为
如何调整和维护 Treap 树,有两种方法,旋转法和 FHQ,两种方法的计算复杂度都为
# 定义节点
struct Node {
int ch[2], siz, val, rnd;
Node(int val = 0, int rnd = 0) : val(val), rnd(rnd) {
ch[0] = ch[1] = 0;
siz = 1;
}
};
2
3
4
5
6
7
# 旋转
我们需要把节点 插入 Treap 树
- 用朴素的方法把 按照键值大小插入一个空的叶子节点
- 给 随机分配一个优先级,如果 的优先级违法了堆的性质,那么让 向上走代替父节点
这里我们调整的过程就用到了一种技巧,树的旋转
这里是 rotate(int o),左旋的话就是右儿子转到原来那个节点的位置
注意:这里的 rotate 和 splay 里面的不一样
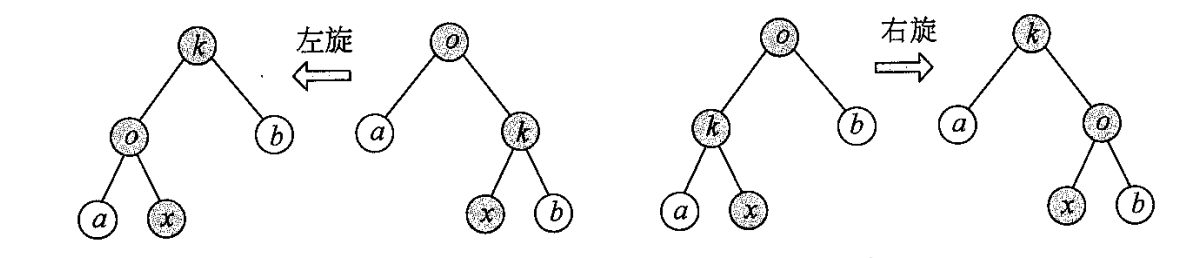
观察到,树的旋转只影响了堆的性质,对于 BST 没有影响
void rotate(int &x, int op) { // op = 0 左旋, op = 1 右旋
int y = t[x].ch[op];
t[x].ch[op] = t[y].ch[op ^ 1];
t[y].ch[op ^ 1] = x;
push_up(x); push_up(y);
x = y;
}
2
3
4
5
6
7
# 插入
void insert(int &x, int val) {
if (!x) {
x = ++tot;
t[x] = Node(val, brand());
return ;
}
t[x].siz += 1;
if (val <= t[x].val) {
insert(t[x].ch[0], val);
if (t[t[x].ch[0]].rnd > t[x].rnd) rotate(x, 1);
}
else {
insert(t[x].ch[1], val);
if (t[t[x].ch[1]].rnd > t[x].rnd) rotate(x, 0);
}
push_up(x);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 删除节点
如果待删除的节点是叶子节点,直接删除,如果待删除的节点 有两个子节点,那么找到优先级大的那个子节点,把 反方向旋转,也就是把 向下调整,直到 被旋转到叶子节点,然后删除
void del(int &x, int val) {
t[x].siz -= 1;
if (val == t[x].val) {
if (t[x].ch[0] == 0 && t[x].ch[1] == 0) { // 如果没有儿子
x = 0;
return ;
}
if (t[x].ch[0] == 0 || t[x].ch[1] == 0) { // 如果只有一个儿子
x = t[x].ch[0] + t[x].ch[1];
return ;
}
if (t[t[x].ch[0]].rnd < t[t[x].ch[1]].rnd) {
rotate(x, 0);
del(t[x].ch[1], val);
return ;
}
else {
rotate(x, 1);
del(t[x].ch[0], val);
return ;
}
}
if (val <= t[x].val) del(t[x].ch[0], val);
else del(t[x].ch[1], val);
push_up(x);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 代码实现
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e6+10;
struct Treap{
int cnt=0,root=0;
struct Node{
int ls,rs; //左儿子,右儿子
int val,pri; //键值,优先级 ,小根堆
int siz; //子树大小
Node(int v=0,int p=0):val(v),pri(p),siz(1),ls(0),rs(0){}
};
vector<Node> t;
Treap(int n) {
t.assign(n+1,Node());
t[0].siz=0;
}
void update(int x){t[x].siz=t[t[x].ls].siz+t[t[x].rs].siz+1;}
void rotate(int &x,int d){ // d=0 右旋,d=1左旋
int k;
if(d==1){
k=t[x].rs;
t[x].rs=t[k].ls;
t[k].ls=x;
}
else{
k=t[x].ls;
t[x].ls=t[k].rs;
t[k].rs=x;
}
t[k].siz=t[x].siz;
update(x);
x=k;
}
void insert(int &x,int val){
if(!x){++cnt;x=cnt;t[x]=Node(val,rand());return ;}
t[x].siz++;
if(val <= t[x].val){
insert(t[x].ls,val);
if(t[t[x].ls].pri > t[x].pri) rotate(x,0);
}
else{
insert(t[x].rs,val);
if(t[t[x].rs].pri > t[x].pri) rotate(x,1);
}
update(x);
}
void del(int &x,int val){
t[x].siz--;
if(val == t[x].val){
if(t[x].ls==0 && t[x].rs==0) {x=0;return ;} //叶子节点,直接删除
if(t[x].ls==0 || t[x].rs==0) {x=t[x].ls+t[x].rs;return ;} //只有一个儿子,直接删除
if(t[t[x].ls].pri < t[t[x].rs].pri) {
rotate(x,0),del(t[x].rs,val);return ;
}
else {
rotate(x,1),del(t[x].ls,val);return ;
}
}
if(val <= t[x].val)
del(t[x].ls,val);
else
del(t[x].rs,val);
update(x);
}
int rank(int x,int val) { // val 的排名
if(x==0) return 0;
if(val <= t[x].val) return rank(t[x].ls,val);
else return t[t[x].ls].siz+1+rank(t[x].rs,val);
}
int kth(int x,int k){ // 排名为 k 的值
if(k==t[t[x].ls].siz+1) return t[x].val;
if(k <= t[t[x].ls].siz) return kth(t[x].ls,k); //在左子树
else return kth(t[x].rs,k-t[t[x].ls].siz-1);
}
int pre(int x,int val){ //val 的前驱
if(x==0) return 0;
if(val <= t[x].val) return pre(t[x].ls,val);
int tmp=pre(t[x].rs,val);
if(tmp==0) return t[x].val;
else return tmp;
}
int nxt(int x,int val){ //val 的后继
if(x==0) return 0;
if(val >= t[x].val) return nxt(t[x].rs,val);
int tmp=nxt(t[x].ls,val);
if(tmp==0) return t[x].val;
else return tmp;
}
};
int main(){
freopen("P3369.in","r",stdin);
freopen("P33690.out","w",stdout);
srand(time(0));
int Q; scanf("%d",&Q);
Treap T(Q);
int op,x;
while(Q--){
scanf("%d%d",&op,&x);
if(op==1) T.insert(T.root,x);
if(op==2) T.del(T.root,x);
if(op==3) printf("%d\n",T.rank(T.root,x)+1);
if(op==4) printf("%d\n",T.kth(T.root,x));
if(op==5) printf("%d\n",T.pre(T.root,x));
if(op==6) printf("%d\n",T.nxt(T.root,x));
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
# FHQ Treap
FHQ 和 旋转法的维护方式不同,但结果是一样的
FHQ Treap 的高明之处是所有操作都只用到了分裂和合并两个操作,这两个操作的复杂度都为
# 分裂
void split(int x,int val,int &L,int &R) 其中 和 是引用传递,函数返回 和 的值,把一颗以 为根的子树按 键值 分裂,返回分别以 , 为根的两颗子树,其中左子树 上所有节点的键值都小于等于 ,右子树 上所有节点的键值都大于
struct Treap{
struct Node{
int ls,rs; //左儿子,右儿子
int val,pri; //键值,优先级
int siz; //子树大小
Node(int v=0,int p=0):val(v),pri(p),siz(1),ls(0),rs(0){}
};
vector<Node> t;
Treap(int n) {t.assign(n+1,Node());t[0].siz=0;}
void split(int x,int val,int &L,int &R){
if(!x){L=R=0;return ;}
if(val < t[x].val){
R=x;
split(t[x].ls,val,L,t[x].ls);
}
else{
L=x;
split(t[x].rs,val,t[x].rs,R);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
其中的 split 函数非常巧妙的利用引用和回溯做到了分裂
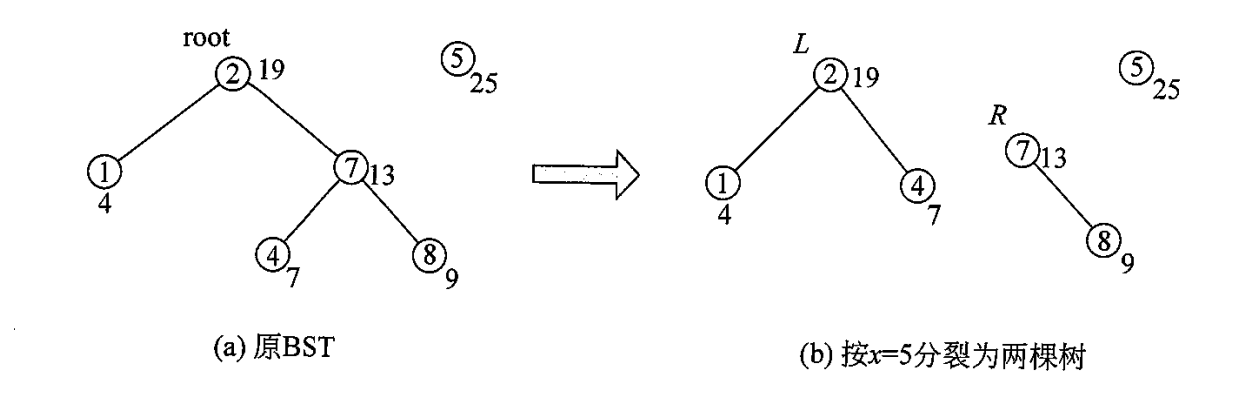
例如, 曾经是 的左节点,但分裂后就变成了 的右节点,就是因为使用了回溯的原因
可以这么理解,例如图中 那么就应该往右儿子走,此时 的优先级肯定是最大的,于是 然后递归调用右儿子,此时 的右儿子已经被拆分成两部分,大于 的和小于 的,引用就是把小于 的那部分添加到 的右儿子上面
# 合并
代码比较简单易懂
void merge(int L,int R){ //合并以 L,R 为根的两棵树,返回合并后的根
if(L==0 || R==0) return L+R;
if(t[L].pri > t[R].pri) { // L 的优先级大于 R 的优先级,L 节点为根
t[L].rs = merge(t[L].rs,R);
return L;
}
else{
t[R].ls = merge(L,t[R].ls);
return R;
}
}
2
3
4
5
6
7
8
9
10
11
# 插入
插入一个新节点,按照新节点 的键值把树分裂成 , 两颗,合并 和 ,然后继续合并 ,得到一颗新的树

# 删除
把树按 分裂为根小于等于 的树 和根大于 的树 ,再把 分裂为根小于 的树 和根等于 的树 ,合并 的左右儿子得到了树 ,也就是删除 ,最后合并
# 排名
排名的代码可以和旋转法一样,但是这里给出一种新的方法
把数按 分裂成 ,其中 中包含所有 的值, 子树的大小 就是 的排名,输出答案后再合并
# 前驱
求比 小的数,把树按 分裂成 和 ,在 中找最大的数,找到后合并
# 后继
求比 大的数,按 分裂成 和 在 数中找最小的数
# 代码实现
#include<bits/stdc++.h>
using namespace std;
struct Treap{
int cnt=0,root=0;
struct Node{
int ls,rs; //左儿子,右儿子
int val,pri; //键值,优先级
int siz; //子树大小
Node(int v=0,int p=0):val(v),pri(p),siz(1),ls(0),rs(0){}
};
vector<Node> t;
Treap(int n) {t.assign(n+1,Node());t[0].siz=0;}
void update(int x){t[x].siz=t[t[x].ls].siz+t[t[x].rs].siz+1;}
void split(int x,int val,int &L,int &R){
if(!x){L=R=0;return ;}
if(val < t[x].val){ //注意这里是 < ,因为当 val == t[x].val 时,也要把 val 放在 L 中
R=x;
split(t[x].ls,val,L,t[x].ls);
}
else{
L=x;
split(t[x].rs,val,t[x].rs,R);
}
update(x); //有可能会改变 x 的左右儿子,所以要更新 x 的 siz
}
int merge(int L,int R){ //合并以 L,R 为根的两棵树,返回合并后的根
if(L==0 || R==0) return L+R;
if(t[L].pri > t[R].pri) { // L 的优先级大于 R 的优先级,L 节点为根
t[L].rs = merge(t[L].rs,R);
update(L); //t[L]的右儿子可能改变,所以要更新
return L;
}
else{
t[R].ls = merge(L,t[R].ls);
update(R); //t[R]的左儿子可能改变,所以要更新
return R;
}
}
void insert(int val){ //插入数字 val
int L,R;
split(root,val,L,R);
++cnt;t[cnt]=Node(val,rand());
root=merge(merge(L,cnt),R);
}
void del(int val){ //删除数字 val
int L,R,p;
split(root,val,L,R); // <= val 的在 L 中,> val 的在 R 中
split(L,val-1,L,p); // < val 的在 L 中,= val 的在 p 中
p=merge(t[p].ls,t[p].rs); //删除 p 节点
root=merge(merge(L,p),R);
}
void rank(int val){ //查询 x 的排名
int L,R;
split(root,val-1,L,R);
printf("%d\n",t[L].siz+1);
root=merge(L,R);
}
int kth(int x,int k){
if(k == t[t[x].ls].siz+1) return x;
if(k <= t[t[x].ls].siz) return kth(t[x].ls,k);
else return kth(t[x].rs,k-t[t[x].ls].siz-1);
}
void pre(int val){
int L,R;
split(root,val-1,L,R);
printf("%d\n",t[kth(L,t[L].siz)].val);
root=merge(L,R);
}
void nxt(int val){
int L,R;
split(root,val,L,R);
printf("%d\n",t[kth(R,1)].val);
root=merge(L,R);
}
};
int main(){
freopen("P3369.in","r",stdin);
freopen("P3369_1.out","w",stdout);
srand(time(0));
int n;scanf("%d",&n);
Treap T(n);
int op,x;
while(n--){
scanf("%d%d",&op,&x);
if(op==1) T.insert(x);
else if(op==2) T.del(x);
else if(op==3) T.rank(x);
else if(op==4) printf("%d\n",T.t[T.kth(T.root,x)].val);
else if(op==5) T.pre(x);
else if(op==6) T.nxt(x);
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
