树相关

树的重心

如果在树中选择某个节点并删除，这棵树将分为若干棵子树，统计子树节点数并记录最大值。取遍树上所有节点，使此最大值取到最小的节点被称为整个树的重心。

（这里以及下文中的「子树」若无特殊说明都是指无根树的子树，即包括「向上」的那棵子树，并且不包括整棵树自身。）

性质

• 树的重心如果不唯一，则至多有两个，且这两个重心相邻
• 以树的重心为根时，所有子树的大小都不超过整棵树大小的一半
• 树中所有点到某个点的距离和中，到重心的距离和是最小的；如果有两个重心，那么到它们的距离和一样
• 把两棵树通过一条边相连得到一棵新的树，那么新的树的重心在连接原来两棵树的重心的路径上
• 在一棵树上添加或删除一个叶子，那么它的重心最多只移动一条边的距离

实现

在 DFS 中计算每个子树的大小，记录「向下」的子树的最大大小，利用总点数 - 当前子树（这里的子树指有根树的子树）的大小得到「向上」的子树的大小，然后让向上的子树和向下最大的子树比较一下得出最大的 "子树"

然后根据定义，最大 "子树" 最小来求出答案

// 这份代码默认节点编号从 1 开始，即 i ∈ [1,n]
int size[MAXN],  // 这个节点的「大小」（所有子树上节点数 + 该节点）
    weight[MAXN],  // 这个节点的「重量」，即所有子树「大小」的最大值
    centroid[2];  // 用于记录树的重心（存的是节点编号）

void GetCentroid(int cur, int fa) {  // cur 表示当前节点 (current)
  size[cur] = 1;
  weight[cur] = 0;
  for (int i = head[cur]; i != -1; i = e[i].nxt) {
    if (e[i].to != fa) {  // e[i].to 表示这条有向边所通向的节点。
      GetCentroid(e[i].to, cur);
      size[cur] += size[e[i].to];
      weight[cur] = max(weight[cur], size[e[i].to]);
    }
  }
  weight[cur] = max(weight[cur], n - size[cur]);
  if (weight[cur] <= n / 2) {  // 依照树的重心的定义统计
    centroid[centroid[0] != 0] = cur;
  }
}

树分块

引言

在大多数时候，树上问题可以使用树剖、动态树和树分治进行解决，但在一些的特殊的情况下，或者在数据范围较为宽松的情况下，树分块也是一种不错的选择

概述

树分块是一种暴力算法， 大致思想就是将树上的点每次划分进 $\sqrt{N}$ (或者基于题目性质的更优块大小)个块中，对与块内信息进行维护的算法

分块方法

法一

按照 DFS 序进行划分，不能保证直径长度和块联通，一般用于处理子树信息，在处理其它信息时较为乏力

法二

检查当前节点的父亲所在块的大小，如果小于 $\sqrt{N}$ 就把当前的节点加进去，如何实现呢，用一个栈存下每个dfs的点，如果和父节点的距离超过块的大小，那么就把 这些点弹出作为一个块

是比较常用的分块方法，缺点就是不能确保块的数量

法三

没看懂，一种随机化算法？？？

树哈希

判断一些树是否同构的时，我们常常把这些树转成哈希值储存起来，以降低复杂度

树哈希的方法有很多，但是有些方法容易被卡掉，下面介绍一种不容易被卡的哈希方法

算法实现

我们需要一个多重集的哈希函数，是一个集合哈希出一个值。以某个结点为根的子树的哈希值，就是以它的所有儿子为根的子树的哈希值构成的多重集的哈希值，即：

$h_x=f(\{h_i|i\in son(x)\})$

其中 $h_x$ 表示以 $x$ 为根的子树哈希值， $f$ 是多重集哈希函数。

以代码中使用的哈希函数为例：

$f(S)=(c+\sum\limits_{x\in S}g(x))\operatorname{mod} m$

其中 $c$ 为常数，一般使用 $1$ 即可。$m$ 为模数，一般使用 $2^{32}$ 或 $2^{64}$ 进行自然溢出，或者使用大素数。$g$ 为整数到整数的映射，代码中使用 xor shift，也可以选用其他的函数，但是不建议使用多项式。为了预防出题人对着 xor hash 卡，还可以在映射前后异或一个随机常数。

这就是一段 xor shift 函数

ull shift(ull x){
    x^=mask;
    x^=x<<13;
    x^=x>>7;
    x^=x<<17;
    x^=mask;
    return x;
}

如果需要换根，第二次 DP 时只需把子树哈希减掉即可

代码实现

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const ull mask=std::chrono::steady_clock::now().time_since_epoch().count();

ull shift(ull x){
    x^=mask;
    x^=x<<13;
    x^=x>>7;
    x^=x<<17;
    x^=mask;
    return x;
}

const int maxn=1e6+5;
int n;
ull hsh[maxn];
vector<int> E[maxn];
set<ull> trees;

void get_hash(int u,int fa){
    hsh[u]=1;
    for(int& v:E[u]){
        if(v==fa) continue;
        get_hash(v,u);
        hsh[u]+=shift(hsh[v]);
    }
    trees.insert(hsh[u]);
}

int main(){
    scanf("%d",&n);
    for(int i=1;i<n;i++){
        int u,v;
        scanf("%d%d",&u,&v);
        E[u].push_back(v);
        E[v].push_back(u);
    }
    get_hash(1,0);
    printf("%lu",trees.size());
    return 0;
}

树上启发式合并

启发式算法是基于人类的经验和直觉感觉，对一些算法的优化

在并查集的按秩合并中，我们把小的集合与大的集合合并，代码如下

void merge(int x, int y) {
  int xx = find(x), yy = find(y);
  if (size[xx] < size[yy]) swap(xx, yy);
  fa[yy] = xx;
  size[xx] += size[yy];
}

在树中，我们把高度小的树成为高度较大的树的子树，这个优化可以称为启发式合并算法

算法实现

来看一个问题

给出一个 $n$ 个节点以 $1$ 为根的树，节点 $u$ 的颜色为 $c_n$。现在对每个结点 $u$ 子树里一共出现了多少种不同的颜色，$n\le 2 \times 10^5$

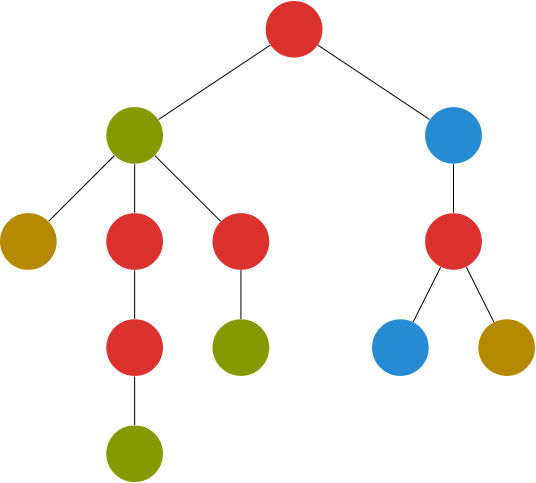
这个问题有很多解决方法，比如树套树，当然如果可以离线，树上莫队也可以，但是树上莫队带根号，可以用 log 实现

既然支持离线，考虑预处理后 $O(1)$ 输出答案，直接暴力预处理的时间复杂度为 $O(n^2)$ ，即对每个子节点进行一次遍历，每次遍历的复杂度显然与 $n$ 同阶，有 $n$ 个结点，故总时间复杂度为 $O(n^2)$

可以发现，每个节点的答案由其子树和其本身得到，考虑利用这个性质处理问题

我们可以处理好重儿子，然后想象让轻儿子 "加" 到重儿子上面

我们用 $cnt[i]$ 表示颜色 $i$ 出现的次数

对于一个节点 $u$：

1. 我们先遍历轻儿子，求出轻儿子的答案，但不保留遍历后它对 $cnt$ 数组的影响
2. 遍历它的重儿子，求出重儿子的答案，保留它对 $cnt$ 数组的影响
3. 再次遍历 $u$ 的轻儿子，在重儿子 $cnt$ 数组上加上轻儿子的贡献，求出 $u$ 的答案

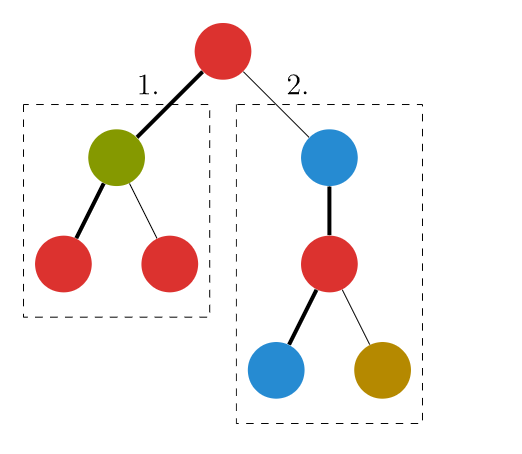
注意，除了重儿子，每次遍历完 $cnt$ 要清零