SOSDP

SOSdp 的全称为 Sum over Subsets dynamic programming 意思就是子集和dp，其实在我看来就是状压dp的一种

我们需要解决这样一个问题：

$F[mask]=\sum\limits_{i\in mask}A[i]$

暴力方法

我们可以 $O(n^4)$ 暴力枚举 $mask$ 和 $i$ 然后查看 $i$ 是不是 $mask$ 的子集

for(int mask =0;mask < (1<<N); ++i){
		for(int i = 0;i < (1<<N); ++i)
			if(i&mask == i)
				F[mask] += A[i];
	}

同理，可以 $O(n^3)$ 枚举所有子集

for(int mask = 0;mask < (1<<N); ++mask){
		F[mask] = A[0];
		for(int i = mask; i > 0; i = (i-1)&mask)
			F[mask] += A[i];
	} 

子集

但是这样的效率都不高，我们定义 $dp[mask][i]$ 代表 $x\&mask=x,x\oplus mask <2^{i+1}$ 的 $A[i]$ 的和，也就是从低到高的前 $i$ 为与 $mask$ 不同 $A[x]$ 的和

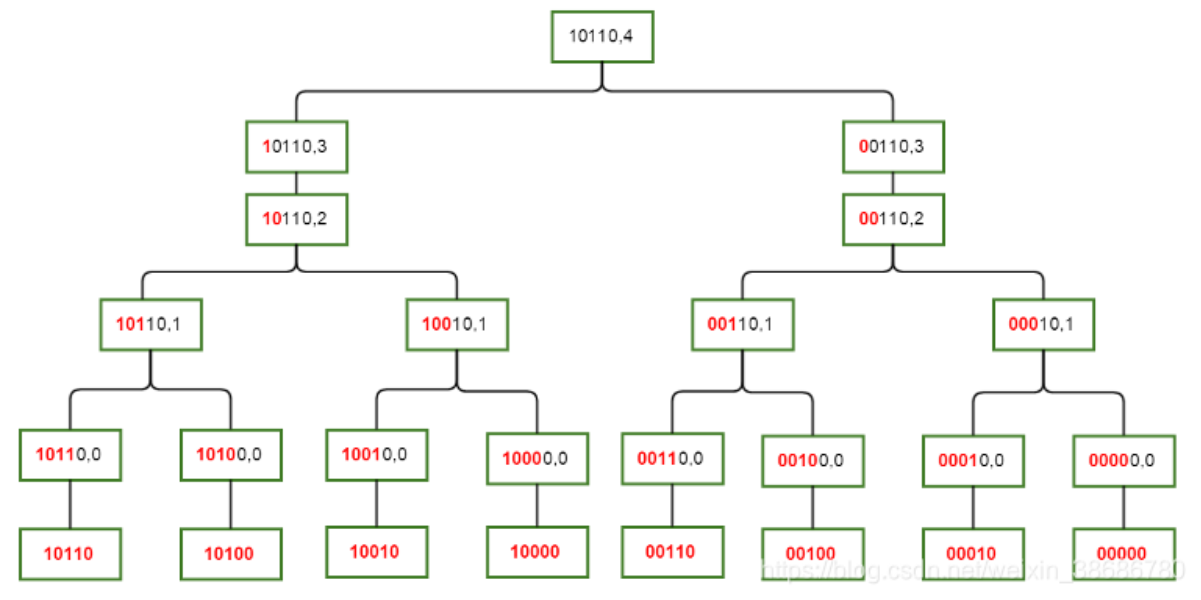
从图中我们能看出转移方程

$\text{dp}[\text{mask}][i] = \begin{cases} \text{dp}[\text{mask}][i - 1] & \text{mask} \& (2^i) = 0 \\ \text{dp}[\text{mask}][i - 1] + \text{dp}[\text{mask} \oplus (2^i)][i - 1] & \text{mask} \& (2^i) = 2^i \end{cases}$

这里利用类似于 01 背包滚动的方法把一维滚掉了

for (int i = 0; i<(1<<N); ++i)
	F[i] = A[i];
for (int i = 0;i < N; ++i) 
	for (int mask = 0; mask < (1<<N); ++mask){
		if (mask & (1<<i)) F[mask] += F[mask ^ (1<<i)];
}

超集

SOSDP 还有另外一种姿势

如果我们需要求：

$F[mask] = \sum\limits_{mask\in i}A[i]$

那么，我们可以对上面那棵树，从上到下 dfs，然后把每个节点的值加到它的子集上

但其实不用这么干，把 01 反转后，子集的关系也翻转了

本来以为自己发现了一个什么奇怪的东西，后面发现这个是超集，超集就是 01 反转后的子集

for (int i = 0;i < N; ++i) 
	for (int mask = 0; mask < (1<<N); ++mask){
		if (!(mask & (1<<i))) F[mask] += F[mask ^ (1<<i)];
}