连通性相关

强连通分量

有向图 $G$ 强连通是指，$G$ 中任意两个结点连通

强连通分量（Strongly Connected Components，SCC）的定义是：极大的强连通子图

在介绍 Tarjan 算法之前，需要了解 DFS 生成树

DFS 生成树

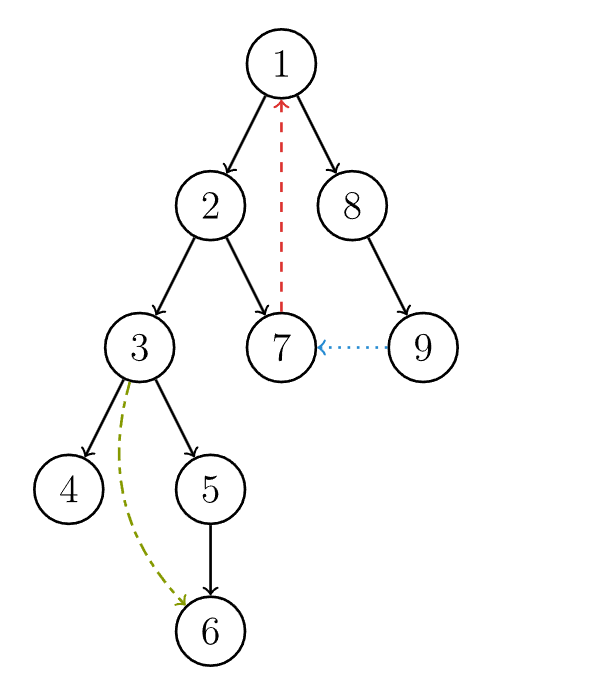
有向图的 DFS 生成树主要有 4 种边（不一定全部出现）：

1. 树边（tree edge）：示意图中以黑色边表示，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边
2. 反祖边（back edge）：示意图中以红色边表示（即 $7 \rightarrow 1$），也被叫做回边，即指向祖先结点的边
3. 横叉边（cross edge）：示意图中以蓝色边表示（即 $9 \rightarrow 7$），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点 并不是 当前结点的祖先
4. 前向边（forward edge）：示意图中以绿色边表示（即 $3 \rightarrow 6$），它是在搜索的时候遇到子树中的结点的时候形成的

我们考虑 DFS 生成树与强连通分量之间的关系

如果结点 $u$ 是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以 $u$ 为根的子树中。结点 $u$ 被称为这个强连通分量的根

Tarjan 算法

在 Tarjan 算法中为每个结点 $u$ 维护了以下几个变量：

1. $dfn_u$：深度优先搜索遍历时结点 u 被搜索的次序
2. $low_u$：在 $u$ 的子树中能够回溯到的最早的已经在栈中的结点。设以 $u$ 为根的子树为 $Subtree_u$。$low_u$ 定义为以下结点的 $dfn$ 的最小值：$Subtree_u$ 中的结点；从 $Subtree_u$ 通过一条不在搜索树上的边能到达的结点

一个结点的子树内结点的 dfn 都大于该结点的 dfn

从根开始的一条路径上的 dfn 严格递增，low 严格非降

按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索，维护每个结点的 $dfn$ 与 $low$ 变量，且让搜索到的结点入栈。

在搜索过程中，对于结点 u 和与其相邻的结点 v（v 不是 u 的父节点）考虑 3 种情况：

1. $v$ 未被访问（树边）：继续对 $v$ 进行深度搜索。在回溯过程中，用 $low_v$ 更新 $low_u$。因为存在从 $u$ 到 $v$ 的直接路径，所以 $v$ 能够回溯到的已经在栈中的结点，$u$ 也一定能够回溯到
2. $v$ 被访问过，已经在栈中（反祖边）：根据 $low$ 的定义，用 $dfn_v$ 更新 $low_u$
3. $v$ 被访问过，且不在栈中（横叉边/前向边）：说明 $v$ 已经搜索完毕，所以不对其做处理

对于一个连通分量，很容易想到，在该连通图中，有且仅有一个 $dfn_v=low_u$。该结点一定是在深度遍历的过程中，该连通分量中第一个被访问过的结点，因为它的 $dfn$ 和 $low$ 值最小，不会被该连通分量中的其他结点所影响

因此，在回溯的过程中，判定 $\textit{dfn}_u=\textit{low}_u$ 是否成立，如果成立，则栈中 u 及其上方的结点构成一个 SCC

struct Tarjan {
    int n; // index from 1
    vector<int> dfn, low, scc, in_stk;
    stack<int> stk;
    int cnt, scc_cnt;

    Tarjan(int n_) {
        n = n_;
        dfn.resize(n + 1); low.resize(n + 1); scc.resize(n + 1); in_stk.resize(n + 1);
        cnt = 0; scc_cnt = 0;
        while (!stk.empty()) stk.pop();
        fill(in_stk.begin(), in_stk.end(), 0);
    }

    void tarjan(int u) {
        low[u] = dfn[u] = ++cnt; stk.push(u); in_stk[u] = 1;
        for (int v : g[u]) {
            if (!dfn[v]) {
                tarjan(v);
                low[u] = min(low[u], low[v]);
            }
            else if (in_stk[v]) low[u] = min(low[u], dfn[v]);
        }
        if (low[u] == dfn[u]) { // 从栈顶到u为一个强连通分量
            scc_cnt++;
            while (true) {
                int x = stk.top(); stk.pop(); in_stk[x] = 0;
                scc[x] = scc_cnt;
                if (x == u) break;
            }
        }
    }
};

割点

对于一个无向图，如果把一个点删除后这个图的极大连通分量数增加了，那么这个点就是这个图的割点（又称割顶）

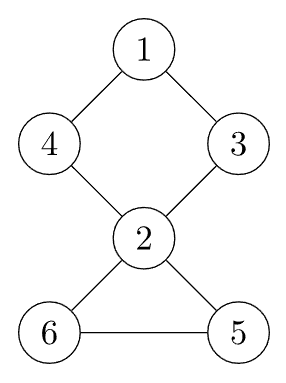
图中，很容易看出割点的个数为 $1$，是 $2$ 结点

首先，我们按照 DFS 序给他打上时间戳（访问的顺序），记在 $dfn$ 数组中

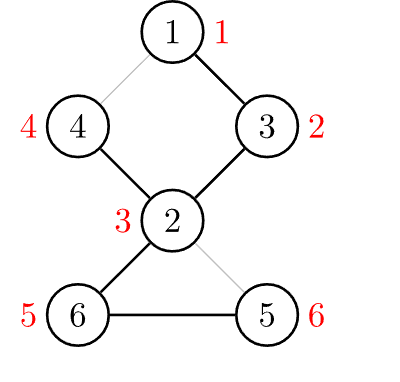
然后需要构造一个 $low$ 数组，用它来存储 不经过其父亲能到达的最小的时间戳，和 Tarjan 求强连通分量的定义一样

例如 $low[2]$ 的话是 $1$，$low[5]$ 和 $low[6]$ 是 $3$

那么，判断一个结点 $u$ 是不是割点：只需要存在一个儿子 $v$，满足 $dfn_u\le low_v$ ，可以这样理解，就是往这个儿子这边走就不可能 "逃" 到 $u$ 的上面了，说明只要删除了 $u$ ，$u$ 的上面部分和这个儿子 $v$ 必然不连通

这个结论对根结点是不适用的，需要特殊处理，如果在生成树中，根结点只有一个儿子，那么就不是割点，否则就是割点

struct Tarjan {
    int n; 
    vector<int> low, dfn, cut;
    int cnt;

    Tarjan(int n_) {
        n = n_; // index = 1
        low.resize(n + 1); dfn.resize(n + 1); cut.clear();
        cnt = 0;
    }

    void tarjan(int u, bool is_root = 1) {
        int sum = 0;
        low[u] = dfn[u] = ++cnt;
        for (int v : g[u]) {
            if (!dfn[v]) {
                tarjan(v, 0);
                low[u] = min(low[u], low[v]);
                if (low[v] >= dfn[u]) sum += 1;
            }
            else 
                low[u] = min(low[u], dfn[v]);
        }
        if (sum >= 2 || (is_root && sum >= 1)) cut.push_back(u); // 如果是根节点，需要判断是否有两个子树
    }
};

割边

对于一个无向图，如果删掉一条边后图中的连通分量数增加了，则称这条边为桥或者割边。

比如说，下图中

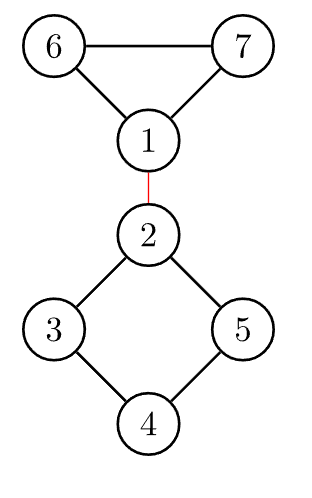
红色的边就是割边

和割点差不多，只要改一处：$low_v>dfn_u$ 就可以了，而且不需要考虑根节点的问题。

对于一个结点 $u$ 的儿子结点 $v$ ，如果满足 $low_v>dfn_u$，说明无法从 $v$ 走到 $u$ 的父节点或者返回 $u$，所以 $u-v$ 这条边就是一条割边

struct Tarjan {
    int n; // index from 1
    vector<int> low, dfn;
    vector<pair<int, int>> bridge;
    int cnt;

    Tarjan(int n_) {
        n = n_;
        low.resize(n + 1); dfn.resize(n + 1);
        cnt = 0; bridge.clear();
    }

    void tarjan(int u, int fa = -1) {
        dfn[u] = low[u] = ++cnt;
        for (int v : g[u]) {
            if (v == fa) continue;
            if (!dfn[v]) {
                tarjan(v, u);
                low[u] = min(low[u], low[v]);
                if (low[v] > dfn[u]) bridge.push_back({u, v});
            } else {
                low[u] = min(low[u], dfn[v]);
            }
        }
    }
};