最近公共祖先

最近公共祖先简称 LCA（Lowest Common Ancestor）。两个节点的最近公共祖先，就是这两个点的公共祖先里面，离根最远的那个。 为了方便，我们记某点集 $S=\{v_1,v_2,\ldots,v_n\}$ 的最近公共祖先为 $\text{LCA}(v_1,v_2,\ldots,v_n) 或 \text{LCA}(S)$

倍增算法

倍增求 LCA 是对朴素算法的改进，通过预处理 $fa[x][i]$ 数组快速向上跳。$fa[x][i]$ 表示点 $x$ 的第 $2^i$ 个祖先。$fa[x][i]$ 可以通过 DFS 预处理出来

算法实现

1. 求出每个点的深度
2. 将 $u,v$ 跳到同一深度。先计算出 $u,v$ 两点的深度之差，设其为 $y$。通过将 $y$ 二进制拆分，每次跳 $y$ 二进制下为 $1$ 的 $2^i$
3. 将 $u,v$ 同时向上跳，如果 $fa_[u][i] \neq fa[v][i]$ ，则$u\gets\text{fa}[u][i]$,$v\gets\text{fa}[v][i]$
4. 最后的 LCA 为 $fa[u][0]$

倍增预处理复杂度为 $O(n\log n)$ ，单词查询时间复杂度为 $O(\log n)$

另外倍增算法可以通过交换 fa 数组的两维使较小维放在前面。这样可以减少 cache miss 次数，提高程序效率

代码实现

#include <bits/stdc++.h>
using namespace std;

const int maxn = 5e5 + 5;
int n, m, rt;
vector<int> g[maxn];
int f[maxn][25], dep[maxn];

void dfs(int u, int fa) {
    f[u][0] = fa;
    dep[u] = dep[fa] + 1;
    for (int i = 1; i <= 20; i++)
        f[u][i] = f[f[u][i - 1]][i - 1];
    for (auto v : g[u]) {
        if (v == fa) continue;
        dfs(v, u);
    }
}

int lca(int x, int y) {
    if (dep[x] < dep[y]) swap(x, y);
    for (int i = 20; i >= 0; i--)
        if (dep[f[x][i]] >= dep[y])
            x = f[x][i];
    if (x == y) return x;
    for (int i = 20; i >= 0; i--)
        if (f[x][i] != f[y][i])
            x = f[x][i], y = f[y][i];
    return f[x][0];
}

int main() {
    ios::sync_with_stdio(false);
    cin >> n >> m >> rt;
    for (int i = 1; i < n; i++) {
        int x, y; cin >> x >> y;
        g[x].push_back(y);
        g[y].push_back(x);
    }
    dfs(rt, 0);
    while (m--) {
        int x, y; cin >> x >> y;
        cout << lca(x, y) << endl;
    }
    return 0;
}

用欧拉序转化成RMQ问题

对一棵树进行 DFS，无论是第一次访问还是回溯，每次到达一个结点时都将编号记录下来，可以得到一个长度为 $2n-1$ 的序列，这个序列被称作这棵树的欧拉序列

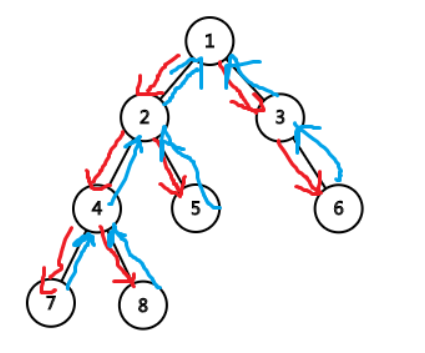
图中的欧拉序为

$1 \rightarrow 2 \rightarrow 4 \rightarrow 7 \rightarrow 4 \rightarrow 8 \rightarrow 4 \rightarrow 2 \rightarrow 5 \rightarrow 2 \rightarrow 1 \rightarrow 3 \rightarrow 6 \rightarrow 3 \rightarrow 1$

我们设节点 $u$ 在欧拉序中第一次出现的位置编号记为 $pos(u)$ ，把欧拉序列记为 $\{E\}$，通过欧拉序，我们可以把 $LCA$ 转化成 RMQ 问题

$LCA(u,v)$ 就是 $E[pos(u)\sim pos(v)]$ 中深度最小的点

用 $RMQ$ 很容易实现区间最值问题

代码实现

#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e5 + 5;

vector<int> g[maxn];

int dep[maxn << 1], lg[maxn << 1], st[maxn << 1][25], dfn[maxn], tot;
int E[maxn << 1];

void dfs (int u, int fa) {
    dfn[u] = ++tot; E[tot] = u;
    dep[u] = dep[fa] + 1;
    for (auto v : g[u]) {
        if (v == fa) continue;
        dfs(v, u);
        E[++tot] = u;
    }
}

void build_st() {
    lg[0] = -1;
    for (int i = 1; i <= tot; i++) lg[i] = lg[i >> 1] + 1;

    for (int i = 1; i <= tot; i++) st[i][0] = E[i];
    for (int j = 1; j <= 20; j++) {
        for (int i = 1; i + (1 << j) - 1 <= tot; i++) {
            int x = st[i][j - 1], y = st[i + (1 << (j - 1))][j - 1];
            st[i][j] = dep[x] < dep[y] ? x : y;
        }
    }
}

int lca (int u, int v) {
    if (dfn[u] > dfn[v]) swap(u, v);
    int l = dfn[u], r = dfn[v];
    int k_ = lg[r - l + 1];
    int x = st[l][k_], y = st[r - (1 << k_) + 1][k_];
    return dep[x] < dep[y] ? x : y;
}

int main() {
    freopen ("P3379.in", "r", stdin);
    ios::sync_with_stdio(false);
    int n, m, rt; cin >> n >> m >> rt;
    for (int i = 1; i < n; i++) {
        int x, y; cin >> x >> y;
        g[x].push_back(y);
        g[y].push_back(x);
    }

    dfs(rt, 0);
    build_st();
    while (m--) {
        int x, y; cin >> x >> y;
        cout << lca(x, y) << endl;
    }
    return 0;
}