并查集

将编号分别为 $1\sim n$ 的 $n$ 个对象划分为不相交集合，在每个集合中，选择其中某个元素代表所在的集合

朴素并查集

初始化

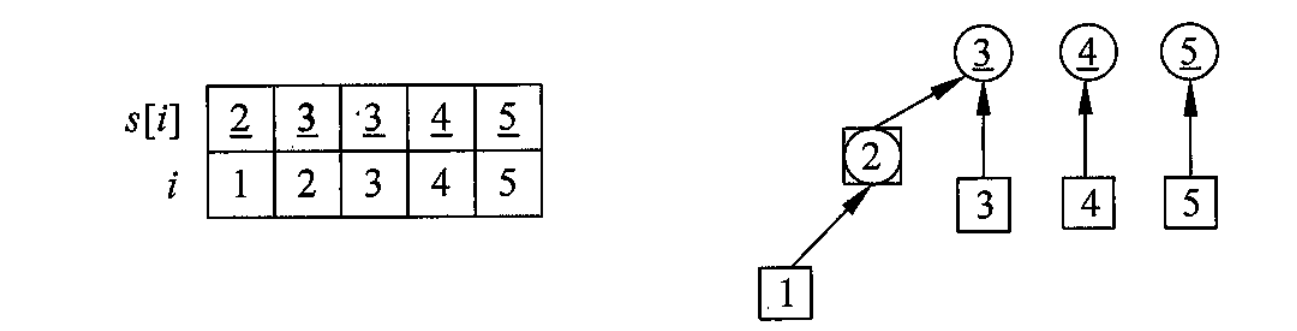
定义 $fa[i]$ 表示元素 $i$ 所属的并查集，我们可以简称为祖先，当初始时，元素的祖先就是他本身

struct dsu{
    int fa[maxn];
    dsu(){for(int i=1;i<=maxn;i++) fa[i]=i;}
}

struct dsu{
    int n;
    vector<int> fa;
    dsu(int n){
        this->n=n;
        fa.resize(n+1);
        for(int i=1;i<=n;i++) fa[i]=i;
    }
};

合并

如果想把 $1,2$ 合并，就把 $1$ 的祖先改为 $2$ 的祖先

然后把 $(1,3)$ 合并，就先找到 $1$ 的祖先 $2$ ，然后找到 $3$ 的祖先，把 $1$ 的祖先和 $3$ 的祖先合并，在这里也就是 $2$ 的祖先变成了 $3$

void merge(int x,int y){
     x=find(x),y=find(y);
     if(x!=y) fa[x]=y;
}

查找

查找就是查找祖先的过程，我们先找自己的祖先，如果自己的祖先不是自己，那么就一直查找下去。可以看到这颗查找树的高度可能很大，复杂度为 $O(n)$，变成了一个链表

int find(int x){
    return fa[x]==x?x:find(fa[x]);
}

合并的优化

注意到查找操作，合并操作的复杂度在极端情况下都为 $O(n)$

如果考虑每次合并的时候，记录元素 $i$ 在查找树中的高度 $h[i]$，每次合并的时候，把高度较小的集合合并到较大的集合上，减小树的高度

struct dsu{
    int n;
    vector<int> fa,h;
    dsu(int n){
        this->n=n;
        fa.resize(n+1);h.resize(n+1);
        for(int i=1;i<=n;i++) fa[i]=i,h[i]=0;
    }
    int find(int x){
        return fa[x]==x?x:find(fa[x]);
    }
    void merge(int x,int y){
        x=find(x),y=find(y);
        if(x==y) return ;
        if(h[x]==h[y]){ //高度相同，随便合并
            h[x]++;
            fa[y]=x;
        }
        else{ //把矮的合并到高的上
            if(h[x]<h[y]) fa[x]=y;
            else fa[y]=x;
        }
    }
};

事实上，一般不需要合并的优化，因为在做了路径压缩之后，附带优化了合并

查询的优化--路径压缩

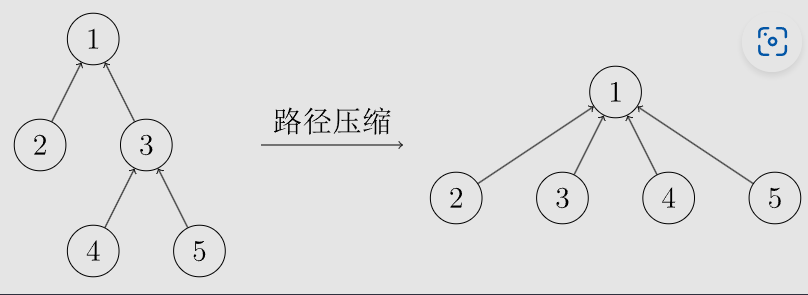
在查询的过程中，搜索的路径可能很长，但是每次查询的结果都是相同的，我们可以在返回时顺便把 $i$ 所属的祖先改为根节点，下次再搜索的时候，就是 $O(1)$ 时间得到结果

int find(){
   return fa[x] == x ? x:fa[x] = getfa(fa[x]);
}

启发式合并

启发式合并就是维护一个 $\text{size}[x]$ 表示以 $x$ 为根的子树大小，每次合并的时候，把小的那个子树链接到大的子树上面

使用启发式合并的时候可以不使用路径压缩，而能保证每次查找祖先节点最多迭代 $\log n$ 次

struct DSU {
    int fa[MAXN], sz[MAXN];
    
    void init(int n) {
        for (int i = 1; i <= n; i++) {
            fa[i] = i;
            sz[i] = 1;
        }
    }

    int find(int x) {
        while (x != fa[x]) {
            x = fa[x];
        }
        return x;
    }
    
    bool same(int x, int y) {
        return find(x) == find(y);
    }
    
    void merge(int x, int y) {
        int fx = find(x), fy = find(y);
        if (fx == fy) return ;
        if (sz[fx] < sz[fy]) swap(fx, fy);
        fa[fy] = fx;
        sz[fx] += sz[fy];
    }
};

可撤销并查集

如果我们需要做到：

1. 合并
2. 查询联通性
3. 撤销上一次操作

就需要用到可撤销并查集了

我们观察上面的启发式合并，发现每次合并其实只修改了两个值，一个是 $fa[fy]$ 和 $siz[fx]$

我们采用两个 vector<pair<int&, int>> 来表示修改后的值和修改前的值，第一维是引用会跟着值之后的修改而修改

如果需要撤销操作，我们只需要把 pair 的前后赋值给前一维就好了

struct DSU {
    int fa[MAXN], sz[MAXN];
    vector<pair<int&, int>> his_fa, his_sz;
    
    void init(int n) {
        for (int i = 1; i <= n; i++) {
            fa[i] = i;
            sz[i] = 1;
        }
    }

    int find(int x) {
        while (x != fa[x]) {
            x = fa[x];
        }
        return x;
    }
    
    bool same(int x, int y) {
        return find(x) == find(y);
    }
    
    void merge(int x, int y) {
        int fx = find(x), fy = find(y);
        if (fx == fy) return ;
        if (sz[fx] < sz[fy]) swap(fx, fy);
        his_fa.emplace_back(fa[fx], fa[fx]);
        his_fa.emplace_back(fa[fy], fa[fy]);
        fa[fy] = fx;
        sz[fx] += sz[fy];
    }

    int history_size() {
        return his_fa.size();
    }

    void roll_back(int h) { // 回滚
        while (his_fa.size() > h) { // 撤销直到 h 操作
            his_fa.back().first = his_fa.back().second;
            his_fa.pop_back();
            his_sz.back().first = his_sz.back().second;
            his_sz.pop_back();
        }
    }
};

例题：

广州大学第十九届ACM大学生程序设计竞赛 L - 提瓦特大陆·元素共鸣之谜 (opens new window)

几乎是板子题了

删除

假设我们要做到这样一些操作

• 删除一个节点，并将它的儿子连接到这个节点的父节点上

• 查询一个节点的祖先节点，如果这个节点已经被删除就不输出

要删除一个叶子节点，我们可以将其父亲设为自己。为了保证要删除的元素都是叶子，我们可以预先为每个节点制作副本，并将其副本作为父亲。

struct dsu{
    int fa[maxn<<1],size[mxan<<1];
    dsu(){
        for(int i = 1; i <= maxn; i++) 
            fa[i] = i + maxn, size[i] = 1;
        for(int i = maxn + 1, i <= mxan; i++)
            fa[i] = i, size[1] = 1;
    }
    void erase(size_t x) {
    	--size[find(x)];
    	pa[x] = x;
  	}
}

移动

与删除类似，通过以副本作为父亲，保证要移动的元素都是叶子

void move(int x,int y){
    int fx=find(x),fy=find(y);
    if(fx==fy)return ;
    fa[fx]=fy;
    --size[fx],++size[fy];
}

带权并查集

有些题需要我们在点之间加上权值

并查集实际上就是在维护若干棵树，并查集的合并和查询优化，实际上就是在改变树的形状，把细长的树变成粗短的树。

带权值的路径压缩

定义 $d[i]$ 表示节点 $i$ 到父节点的权值

在路径压缩时，$d$ 数组时累加关系，定义 $d'$ 时修改后的 $d$ 数组，也就是 $d[1]'=d[1]+d[2]+d[3]$，在具体的题目中，可能由相乘，异或等其他操作

带权值的合并

合并的操作中，把点 $x$ 与点 $y$ 合并，就是把 $x$ 的祖先 $fx$ 合并到 $y$ 的祖先 $fy$ 中，然后在 $fx$ 和 $fy$ 之间添加权值

具体怎么写要视情况而定