 第一章:递归问题
第一章:递归问题
# 河内塔问题
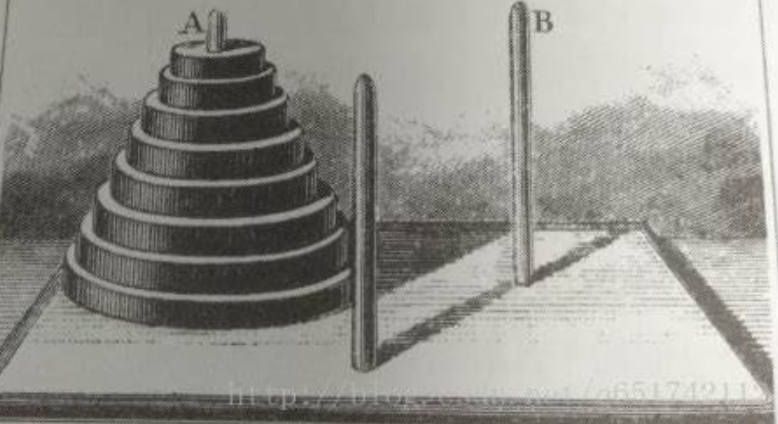
有 根柱子和 个圆盘,我们可以把最顶上的圆盘移到另外的柱子上,但不可以把大的圆盘放在小的圆盘上面
问,最少需要多少步才能把所有圆盘从一根柱子移到另外一跟柱子上
我们先命名一个状态 表示圆盘从一根柱子移动到另外一根柱子的最少次数
那么我们思考一种移动方案,假设我们要把圆盘从 柱移动到 柱上
那么我们可以将 个圆盘移动 柱上 然后把最下面的圆盘移动到 柱上,最后把 个圆盘从 柱移到 柱,所以,我们能得到方程
我们想要得到通项公式,可以盲猜结论
可以用数学归纳法证明
- 时等式成立
- 时,假设 成立,可得
证毕
# 平面上的直线
平面上 条直线所界定的区域最大个数 是多少
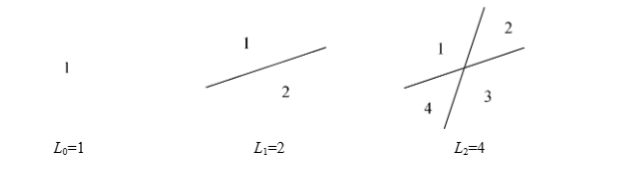
我们考虑假设已经有 条直线,我们需要画一条直线,这条直线最多和 条直线相交产生 个新的区域
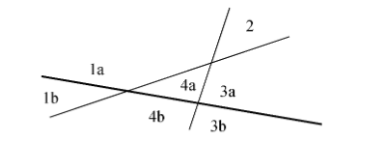
所以我们得到了
很容易我们可以得出
考虑一个变形,平面上由 条这样的折线所界定区域的最大的个数 是多少
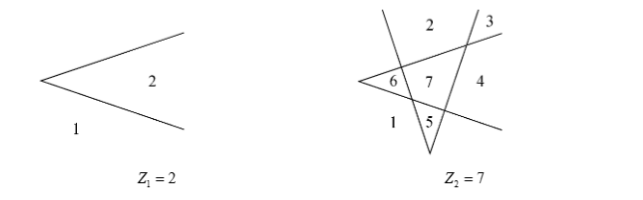
考虑一个折线可以看作两条直线擦掉一半,对于每个折线,我们都失去了 块区域
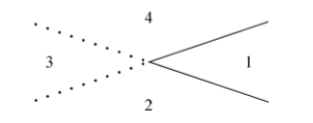
所以
# 约瑟夫问题
从围成标有记号的 到 的 个人开始,每隔一个删去一个人,直到有一个人幸存下来
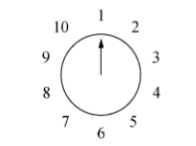
时,消去的人时 最后 幸存
我们由此能得到几个规律:
- 每一轮杀人,杀一半,向下取整,偶数编号的人会被杀
- 幸存的人,重新编号
# 递归表达式
每轮杀人,编号减半,那么最后肯定剩下一个人,我们能不能从第 轮活下来的那个人的编号反推出第 轮活下来的那个人的编号呢?
设 个人时的幸存的号码为
先考虑偶数的情况,第一圈把偶数的去掉,奇数留下来,假设一开始有 个人,第一轮后就是
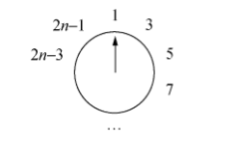
所以我们得到了一个子问题,用递归的思想,假设子问题以及求解完成了,我们可以得到表达式 ,也就是说,存活的那个人的编号是子问题的答案的编号的两倍减一
然后考虑奇数,对于 个人
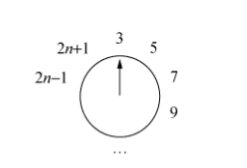
我们得到
所以我们得到了表达式
我们通过这个式子就可以快速得到答案了
接下来尝试把递归式子转化为非递归的形式
# 二进制形式性质
有了递归式,我们能做出一张表:
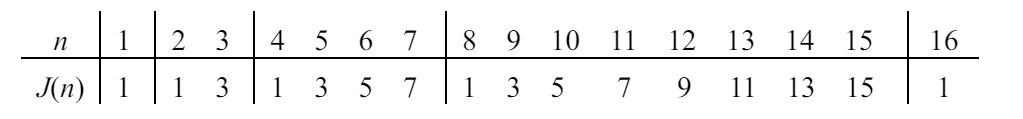
显然可以看出, 按照 为分段,段内为一个等差数列,于是我们能写出 的封闭形式,设 ,则:
我们把 转化成二进制会发现更多规律,不妨设
由于首位字母 必为 ,所以 ,那么
所以
用计算机程序设计的行话说就是, 向左循环移动一位就得到
# 成套方法
我们尝试把 函数进行拓展,有一个类似于 的递归式,引入常数
我们可以构造出如下表:
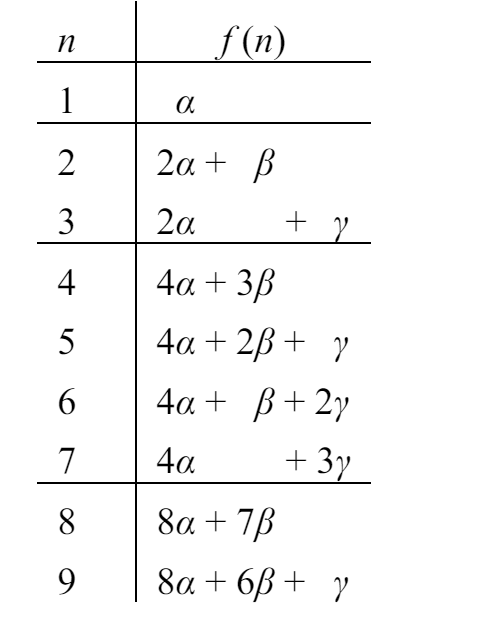
可以观察出 的系数是不超过 的 的最大幂, 的系数递减 , 的系数递增
我们可以得到 的封闭形式:
且我们观察出
这里可以使用数学归纳法证明,但是也可以采用特殊值法来证明,书上把这种方法称为成套方法
由于 的关系在任何情况下都是固定的,所以理论上来说 可以取任意值
不妨取 ,,由:
很显然可以得到
我们还可以设 ,有:
解出来得到 ,于是得到了一个关系式
然后设 ,有:
解出来得到 ,于是得到了一个关系式
联立三个式子:
于是 就可以被解出来了,这就是成套方法
有多少个独立的参数,我们就需要多少个特殊的值,本题中有三个
# 推广的约瑟夫递归式
前面我们得到了一个二进制下循环移位的性质,那么推广的约瑟夫表达式是否也有类似的性质呢?
推广的递归式的形式如下:
展开就是
所以我们可以解除二进制的限制,这里的 一点是 ,但 可以不为
我们把上面的表格换一种形式就可以看出
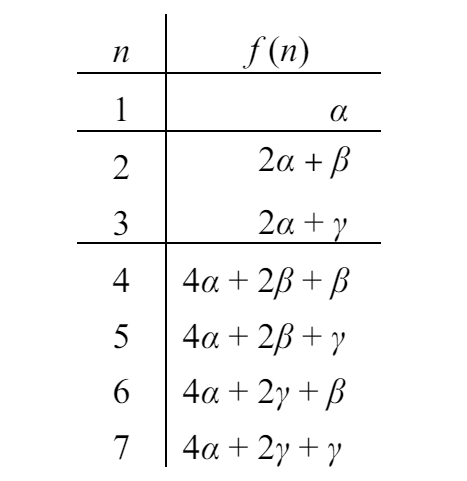
完全符合上面的形式,这里的
于是,我们可以考虑推广基数,这里我们设基数为
这个的解是:
例如,我们有递归式:
假设我们这里要计算 ,有 , ,我们可以把 转化成三进制 ,这里的 ,所以
