数论

素数

素数的定义为只能被 $1$ 和自己整除的正整数

素数的判定

小素数时，使用试除法，大素数时使用 Miller_Rabin 算法

欧拉筛

欧拉筛是一种线性筛，它能在 $O(n)$ 的线性时间内求得 $1\sim n$ 内所有素数

欧拉筛的基本原理，一个合数肯定有一个最小质因数，让每个合数只被它的最小质因数筛一次

1. 检查 $2\sim n$ 如果没有被筛过，那么就是素数
2. 检查到 $i$ 的时候，利用已经求的的素数去筛掉对应的合数 $x$，而且是用 $x$ 的最小质因数去筛

#include <bits/stdc++.h>
using namespace std;
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    int n, q;
    cin >> n >> q;
    vector<int> p;
    vector<bool> vis(n + 1, 0);
    for (int i = 2; i <= n; i++ ){
        if (!vis[i]) p.push_back(i);
        for (int j = 0; j < p.size() && i * p[j] <= n); j++) { // p[j] 就是最小的质因数
            vis[i * p[j]] = 1;
            if (i % p[j] == 0) break;
        }
    }
    while (q--) {
        int x;
        cin >> x;
        cout << p[x - 1] << '\n';
    }
    return 0;
}

分解质因数

显然，我们很容易写出 $O(\sqrt{N})$ 的朴素算法

std::vector<int> breakdown(int x) {
    std::vector<int> res;
    for (int i = 2; i * i <= x; i++) {
        if (x % i == 0) {
            res.push_back(i);
            while (x % i == 0) x /= i;
        }
    }
    if (x != 1)
        res.push_back(x);
    return res;
}

如果提前打出了素数表，那么时间复杂度为 $O(\sqrt{\frac{N}{\ln N}})$

一元线性同余方程

设 $x$ 是未知数，求整数 $x$ 满足 $ax \equiv b \ (mod \ m)$

不妨设 $ax-b$ 是 $m$ 的 $-y$ 倍，则 $ax-b = -my \Rightarrow ax+my = b$

这里就转化成了二元线性丢番图方程了

逆元

给定整数 $a$，满足 $\gcd(a,m) =1$ 称 $ax \equiv 1\ (mod \ m)$ 的一个解为 $a$ 模 $m$ 的逆，记为 $a^{-1}$

如何求逆

小费马定理求逆元

小费马定理： $a^{p-1} \equiv 1 \pmod{m}$

如果在两边同时乘 $a^{-1}$ 得 $a^{p - 2} \equiv a^{-1} \pmod{m}$

拓展欧几里得求逆元

即解同余方程 $ax \equiv 1 \pmod{p}$

拓展欧几里得

裴蜀定理

如果 $a$ 与 $b$ 均为整数，则有整数 $x$ 和 $y$ 使得 $ax + by = \gcd(a,b)$

线性丢番图方程

先来看二元线性丢番图方程

$ax + by = c$

设 $d = \gcd(a,b)$ 如果 $d$ 不能整除 $c$，那么方程没有整数解，如果 $d$ 可以整除 $c$，则方程有无数个整数解

如果存在一个整数解满足 $ax_0 + by_0 = c$ 那么通解就是 $x = x_0 + (b/d)n,y=y_0-(a/d)n$，其中 $n$ 为任意整数

这里可以把 $(b/d)$ 看成 $\Delta x$，把 $\Delta y=(a/d)$

拓展欧几里得算法

我们可以使用拓展欧几里得算法来得到二元线性丢番图方程的一个解

首先我们先考虑解出 $ax+by = \gcd(a,b)$

基本想法是在辗转相除法中，使用 $bx_0 + (a \% b) y_0 = c$ 的解，来得出 $ax + by = c$ 的解

前者等于 $bx_0 + (a - b\lfloor a/b \rfloor y_0) = ay_0 + b(x_0 - \lfloor a/b \rfloor y_0) = c$

对比系数可得 $x = y_0, y = x_0 - \lfloor a/b \rfloor y_0$

辗转相除法时，当 $b=0$ 时递归结束，显然此时 $x = 1, y = 0$

ll exgcd(ll a, ll b, ll &x, ll &y) {
    if (!b) {
        x = 1, y = 0;
        return a;
    }
    LL d = exgcd(b, a % b, x, y), x0 = x, y0 = y;
    x = y0, y = x0 - a / b * y0;
    return d;
}

此时，我们得到了 $ax + by =\gcd(a,b)$ 的一组解，只需要在两边同时乘上 $\frac{c}{\gcd(a,b)}$ 就能得到 $ax+by = c$ 的一组解了

积性函数

如果对任意两个互素的正整数 $p,q$ 有 $f(pq)=f(p)f(q)$ ，$f$ 称为积性函数

积性函数有一个性质，积性函数的和函数也是积性函数。如果 $f$ 是积性函数，那么 $f$ 的和函数 $F(n)=\sum\limits_{d|n}f(d)$ 也是积性函数

如果 $f(n),g(n)$ 是积性函数，则 $h(n)=f(n)g(n)$ 也是积性函数

常见的积性函数

• $1(n)$ ，$1(n)=1$
• $id(n)$ 单位函数，$id(n) = n$
• $I_k(n)$ 幂函数，$I_k(n)=n^k$
• $\varepsilon(n)$ 原函数 $\varepsilon(n)=[n=1]$
• $\sigma(n)$ 因数和函数，$\sigma(n)=\sum\limits_{d|n}d$
• $d(n)$ 约数个数，$d(n)=\sum\limits_{d|n}1$

因为积性函数的性质，我们可以考虑把 $n$ 质因数分解来求积性函数的第 $n$ 项的值

理论上来说，也可以使用欧拉筛来求出 $1\sim n$ 的所有值

欧拉函数

欧拉函数 $\phi(n)$ 定义为不超过 $n$ 且 与 $n$ 互素的正整数的个数

$\phi(n) = \sum\limits_{i=1}^n[\gcd(i,n)=1]$

欧拉反演：

$n = \sum\limits_{d|n}\phi(d)$

计算 $\phi(n)$ 的通解公式

设 $n = p_1^{a_1}\times p_2^{a_2}\times \cdots \times p_k^{a_k}$，有

$\phi(n)=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots(1-\frac{1}{p_k})$

用欧拉晒求 $1\sim n$ 内的所有欧拉函数

通过积性函数的性质 $\phi(p_1p_2)=\phi(p_1)\phi(p_2)$ 求得，$\phi(p_1)$ 和 $\phi(p_2)$ 后可以得出 $\phi(p_1p_2)$

在欧拉筛的时候，$i\times p_j$ 中 $\phi(i)$ 和 $\phi(p_j)$ 都是已知的

vector<int> get_phi (int n) {
    vector<int> phi (n + 1);
    vector<bool> vis (n + 1, 0);
    vector<int> prime;
    for (int i = 2; i <= n; i++) {
        if (!vis[i]) {
            vis[i] = 1;
            prime.push_back(i);
            phi[i] = i - 1;
        }
        for (int j = 0; j < prime.size(); j++) {
            if (i * prime[j] > n) break;
            vis[i * prime[j]] = 1;
            if (i % prime[j] == 0) {
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }
            phi[i * prime[j]] = phi[i] * phi[prime[j]];
        }
    }
    return phi;
}

莫比乌斯函数

莫比乌斯函数的定义为：

$\mu(n) =\begin{cases}1,\ n = 1\\(-1)^r,\ n=p_1p_2\cdots p_n\\0, \ \text{others} \end{cases}$

$\mu(n)$ 是一个积性函数

莫比乌斯函数的和函数：

$\sum\limits_{d|n} \mu(d)=\begin{cases}1, n=1\\0,n=0\end{cases}=[n=1]=\varepsilon(n)$

证明：

设 $n=\prod\limits_{i=1}^k p_i^{c_i},n'=\prod\limits_{i=1}^k p_i$，那么有

$\sum_{d \mid n} \mu(d) = \sum_{d \mid n'} \mu(d) = \sum_{i=0}^{k} \binom{k}{i} \cdot (-1)^i = (1 + (-1))^k$

可以看出，当且仅当 $k=1$ 也就是 $n=1$ 时，式子等于 $1$，其他情况下都等于 $0$

莫比乌斯反演：若 $f$ 是算数函数，$F$ 为 $f$ 的和函数，对任意正整数 $n$，满足 $F(n)=\sum\limits_{d|n}f(d)$，有

$f(n)=\sum\limits_{d|n}\mu(d)F(\frac{n}{d})$

莫比乌斯反演不需要 $f$ 是积性函数，运用莫比乌斯反演可以将一些函数转化，从而降低计算难度

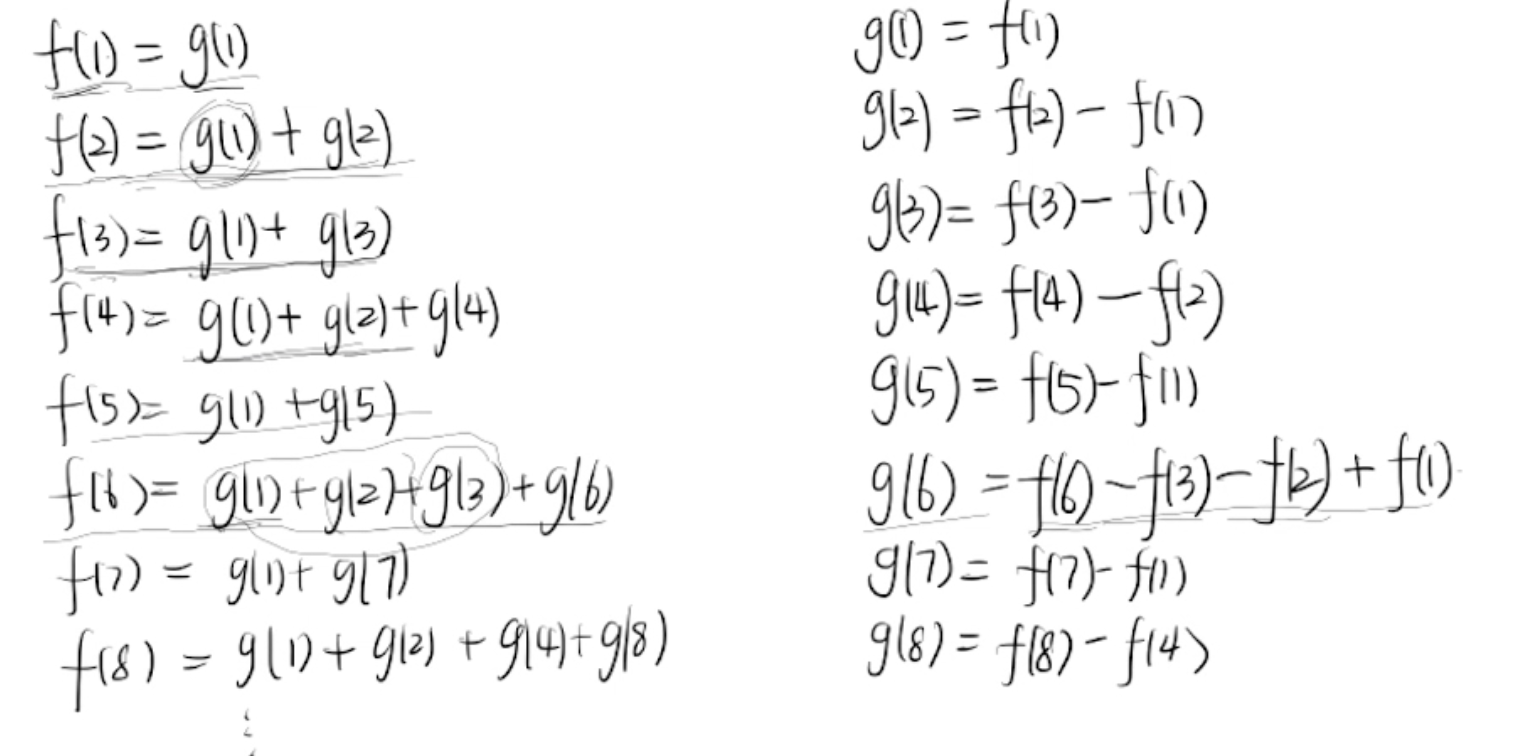
e.g. 假设 $n$ 个元组成一个环，每个元都是 $1,2,\cdots,r$ 中的一个数，两个环不同当且仅当它们不能通过旋转使得两个环中对应的元素都相等，求有多少个这样的环

在现实题目中，比较常用的是莫比乌斯反演的另外一种形式

设 $f,g$ 且存在正整数 $N$，保证 $n>N$ 有 $f(n)=g(n)=0$，则

$f(n)=\sum\limits_{n|m}g(m)\Longleftrightarrow g(n)=\sum\limits_{n|m} \mu(\frac{m}{n})f(m)$

狄利克雷卷积

设 $f$ 和 $g$ 是算术函数，记 $f$ 和 $g$ 的狄利克雷卷积为 $f\ast g$ ，定义为

$(f\ast g)(n)=\sum\limits_{d|n}f(d)g(\frac{n}{d})$

两个积性函数的狄利克雷卷积仍然是积性函数

莫比乌斯反演很容易写成狄利克雷卷积的形式

$f=g\ast 1\Longleftrightarrow g=f\ast \mu$

狄利克雷卷积满足交换律和结合率

考虑一些公式

• $\varepsilon=\mu \ast 1$
• $\text{id}=\phi \ast 1$
• $\phi =\mu \ast \text{id}$

杜教筛

杜教筛用于在低于线性时间里高效求解一些积性函数的前缀和

设 $f(n)$ 是一个数论函数，计算 $S(n) = \sum\limits_{i=1}^n f(i)$

构造两个积性函数 $h$ 和 $g$ ，满足 $h=g\ast f$，根据卷积的定义，有：

$h(i)=\sum\limits_{d|i}g(d)f(\frac{i}{d})$

对 $h(i)$ 求和，有

$\begin{aligned}\sum_{i=1}^n h(i) &=\sum_{i=1}^n\sum_{d|i}^i g(d)f(\frac{i}{d})\\ &=\sum_{d=1}^ng(d)\sum_{d|i}^n f(\frac{i}{d}) \\ &= \sum\limits_{d=1}^ng(d)\sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor} f(i)\\ &= \sum\limits_{d= 1}^n g(d)S(\lfloor\frac{n}{d}\rfloor ) \end{aligned}$

得到

$\sum_{i=1}^n h(i)=\sum\limits_{d= 1}^n g(d)S(\lfloor\frac{n}{d}\rfloor)$

为了计算 $S(n)$，把等式右边的第 $1$ 项提出来，得到

$\sum\limits_{i=1}^n h(i)=g(1)S(n)+\sum\limits_{d=2}^n g(d)S(\lfloor\frac{n}{d}\rfloor)$

$g(1)S(n)=\sum\limits_{i=1}^n h(i)- \sum\limits_{d=2}^n g(d)S(\lfloor\frac{n}{d}\rfloor)$

式子中 $i$ 和 $d$ 无关

$g(1)S(n)= \sum\limits_{i=1}^n h(i)- \sum\limits_{i=2}^n g(i)S(\lfloor\frac{n}{i}\rfloor)$

int prime[maxn];
bool vis[maxn];
int mu[maxn];
LL phi[maxn];

unordered_map <int, int> mu_sum;
unordered_map <int, LL> phi_sum;

void init() {
    int cnt = 0;
    vis[0] = vis[1] = 1;
    mu[1] = phi[1] = 1;
    for (int i = 2; i < maxn; i++) {
        if (!vis[i]) {
            prime[cnt++] = i;
            mu[i] = -1;
            phi[i] = i - 1;
        }
        for (int j = 0l; j < cnt && i * prime[j] < maxn; j++) {
            vis[i * prime[j]] = 1;
            if (i % prime[j] == 0) {
                mu[i * prime[j]] = 0;
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }
            mu[i * prime[j]] = -mu[i];
            phi[i * prime[j]] = phi[i] * phi[prime[j]];
        }
    }
    for (int i = 1; i < maxn; i++) {
        mu[i] += mu[i - 1];
        phi[i] += phi[i - 1];
    }
}

int g_sum(int x) {
    return x;
}

LL get_mu_sum (int x) {
    if (x < maxn) return mu[x];
    if (mu_sum.count(x)) return mu_sum[x];
    LL ret = 1;
    for (LL l = 2, r; l <= x; l = r + 1) {
        r = x / (x / l);
        ret -= 1ll * (r - l + 1) * get_mu_sum(x / l);
    }
    return mu_sum[x] = ret;
}

LL get_phi_sum (int x) {
    if (x < maxn) return phi[x];
    if (phi_sum.count(x)) return phi_sum[x];
    LL ret = 1ll * x * (x + 1) / 2;
    for (LL l = 2, r; l <= x; l = r + 1) {
        r = x / (x / l);
        ret -= 1ll * (r - l + 1) * get_phi_sum(x / l);
    }
    return phi_sum[x] = ret;
}

卢卡斯定理

卢卡斯定义用于计算组合数取模，即求 $C_n^r \mod m$，其中 $m$ 为素数

编程时常用的卢卡斯定理的形式：

$C_n^r \equiv C_{n\mod m}^{r\mod m}\cdot C_{n/m}^{r/m}\pmod m$

数论分块

当研究 $\sum\limits_{i = 1}^n\lfloor \frac{n}{i} \rfloor$ 时，暴力求解是 $O(n)$ 的，但是我们发现 $\lfloor \frac{n}{i}\rfloor$ 的取值只有少数个

我们如果能把他们分块一起累计就好了

对于每个块，可以证明 $L,R$ 满足 $R = n/(n/L)$

现在考虑如何快速计算 $\sum\limits_{i=\text{start}}^\text{end}\lfloor \frac{num}{i} \rfloor$

// for(int i = st;i<=ed;i++)ans+=num/i
int block(int st, int ed, int num) {
	//sum(num/i i in [st,ed])
	int R = 0;
	int _ans = 0;
	ed = min(ed, num);
	for (int L = st; L <= ed; L = R + 1) {
		R = min(ed, num / (num / i));  //该区间的最后一个数;
		_ans += (R - L + 1)*(num / i); //区间 [L,R] 的 num/i 都是一个值
	}
	return _ans;
}

来看一道例题

codeforces 616E (opens new window)

::: notes

给定两个整数 $n,m$ 求

$\sum_{i=1}^m n \ \text{mod} \ i$

• $n,m \le 10^{13}$
• 答案对 $10^9+7$ 取模

:::

把取模写成整除的模式

$\begin{aligned} \sum_{i=1}^m n \ \text{mod} \ i & = \sum_{i=1}^m n-\lfloor \frac{n}{i}\rfloor \times i\\ &=n \times m - \sum_{i=1}^m \lfloor \frac{n}{i}\rfloor \times i \end{aligned}$

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll MOD = 1e9 + 7;

ll qpow(ll a, ll b, ll mod) {
    ll res = 1;
    while (b) {
        if (b & 1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

int main() {
    ll n, m; cin >> n >> m;
    int inv2 = qpow(2, MOD - 2, MOD);
    ll ans = 0;
    ll all = n * m % MOD;
    m = min(m, n);
    for (ll L = 1, R; L <= m; L = R + 1) {
        R = min(m, n / (n / L));
        ll len = R - L + 1;
        ll now = (R + L) % MOD * (R - L + 1) % MOD * inv2 % MOD;
        ans = (ans + now * (n / L) % MOD) % MOD;
    }
    cout << (all - ans + MOD) % MOD << endl;
    return 0;
}

威尔逊定理

若 $p$ 为素数，则 $p$ 可以整除 $(p - 1)! + 1$

$(p - 1)!\equiv -1 \pmod{m}$

BSGS 大步小歩算法

BSGS 常用于求解离散对数，该算法可以在 $O(\sqrt{p})$ 的时间内求解

$a^x\equiv b\pmod{p}$

其中要求 $\gcd(a,p)=1$，方程解满足 $0\le x < p$

令 $x=A\lceil \sqrt{p}\rceil -B$，其中 $0\le A,B \le \lceil \sqrt{p}\rceil$，则有 $a^{A\lceil \sqrt{p}\rceil -B}\equiv b\pmod{p}$

变换一下有 $a^{A\lceil \sqrt{p}\rceil}\equiv ba^B\pmod{p}$

已知 $a,b$ 暴力枚举 $B$，把 $ba^B$ 用 unoreder_map 存下来，然后枚举 $A$，去 map 中配对，从而得到一个解

枚举 $A,B$ 均小于 $\lceil \sqrt{p}\rceil$ 所以时间复杂度为 $O(\sqrt{p})$

求指标

已知 $a,b$ 求

$x^a\equiv b\pmod{p}$

其中 $p$ 是个质数

根据原根的知识：$g^c\equiv x \pmod{p}$ 则称 $x$ 的指标为 $c$，记作 $\text{ind}(x)=c$

所以也就是要求 $(g^c)^a\equiv b\pmod{p}\Rightarrow(g^a)^c\equiv b\pmod{p}$ ，我们已知 $g,a,b$ ，求 $c$，就转化成第一种模型了