组合数学

容斥原理

容斥原理的简单形式，设 $A$ 和 $B$ 是分别具有性质 $P_1$ 和 $P_2$ 的有限集，有

$A\cup B =|A|+|B|-|A\cap B|$

e.g. 求正整数 $1$ 到 $n$ 中，既不是 $2$ 的倍数也不是 $3$ 的倍数的数的个数

设 $S=\{1,2,\cdots ,n\}$，$A$ 是 $2$ 的倍数，$B$ 是 $3$ 的倍数，那么答案就是 $|S|-|A\cup B|$

由于 $|A\cup B|=|A|+|B|-|A\cap B|$， 所以答案就是 $n-\lfloor \frac{n}{2}\rfloor -\lfloor \frac{n}{3}\rfloor +\lfloor \frac{n}{6}\rfloor$

e.g. 求由 $n$ 个元素 $1,2,\cdots,n$ 全排列中，满足 $1$ 和 $2$ 不相邻，$3$ 和 $4$ 不相邻的排列数

设 $A$ 是 $1$ 和 $2$ 相邻，$B$ 是 $3$ 和 $4$ 相邻，那么答案就是 $n!-|A\cup B|$

所以答案就是 $n!-2(n-1)!-2(n-1)!+4(n-2)!$

考虑三个子集的容斥原理

$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$

推广到 $n$ 个集合

设 $S$ 是一个有限集，$A_1,A_2,\cdots ,A_n$ 是 $S$ 的 $n$ 个子集，那么

$|A_1\cup A_2\cup \cdots \cup A_n|=\sum_{i=1}^n(-1)^{i-1}\sum_{1\leq j_1<j_2<\cdots <j_i\leq n}|A_{j_1}\cap A_{j_2}\cap \cdots \cap A_{j_i}|$

我们对答案取补集的形式也很常见：

$S-|A_1\cup A_2\cup \cdots \cup A_n|=\sum_{i=0}^n(-1)^{i}\sum_{1\leq j_1<j_2<\cdots <j_i\leq n}|A_{j_1}\cap A_{j_2}\cap \cdots \cap A_{j_i}|$

这里需要定义 $|\cap \varnothing|=S$

e.g. $m$ 件不同的物品，分配给 $n$ 个人，要求每个人至少要分得一件物品，求不同的分配方案数

设 $S=$ 总方案数，$A_i=$ 第 $i$ 个人没有分到物品的方案数

答案就是

$S-|A_1\cup A_2\cup \cdots \cup A_n|=\sum_{i=0}^n(-1)^{i}\sum_{1\leq j_1<j_2<\cdots <j_i\leq n}|A_{j_1}\cap A_{j_2}\cap \cdots \cap A_{j_i}|$

$|A_{j_1}\cap A_{j_2}\cap \cdots \cap A_{j_i}|$ 就是 $n-i$ 个人分配 $m$ 件物品的方案数，即 $C(n,n-i)\times (n-i)^{m}=C(n,i)\times (n-i)^{m}$

得到了答案的递推式：

$\sum_{i=0}^n(-1)^{i}C(n,i)\times (n-i)^{m}$

e.g. 错排问题：$p$ 是一个排列，满足 $p_i\neq i$ 的数的个数称为错排数，求错排数

设 $S$ 是所有排列数，$A_i$ 是 $i$ 不在 $p_i$ 的位置的排列数

$|S-\cup^{n}_{i=1} A_i|=\sum_{i=0}^{n}C_{n}^i(n-i)!$

容斥原理的符号形式

设 $S$ 是一个有限集，$a_1,a_2,\cdots, a_n$ 是 $n$ 种性质

• 记 $N(a_i)$ 为 $S$ 中有 $a_i$ 性质的元素的数量。特殊的，记 $N(1)=|S|$
• 记 $N(1-a_i)$ 为 $S$ 中没有 $a_i$ 性质的元素的数量
• $N(a_{i_1},a_{i_2},\cdots,a_{i_k})$ 为 $S$ 中同时有 $a_{i_1}, a_{i_2},\cdots,a_{i_k}$，性质的元素的数量
• 记 $N(a+b)=N(a)+N(b)$

通过符号形式，我们可以把容斥原理改成多项式来处理

则，容斥原理可以写成：

$N((1-a_1)(1-a_2)\cdots(1-a_n))=\sum\limits_{i=0}^n(-1)^i \ \sum\limits_{1\le j_1<j_2<\cdots<j_i\le n} N(a_{j_1},a_{j_2},\cdots,a_{j_i})$

e.g. 求正整数 $1$ 到 $n$ 中，既不是 $2$ 的倍数，也不是 $3$ 的倍数，但是 $5$ 的倍数的数的数量

设 $a_1$ 设 $2$ 的倍数，$a_2$ 是 $3$ 的倍数， $a_3$ 是 $5$ 的倍数

答案就是 $N((1-a_1)(1-a_2)a_3)=N(a_3-a_1a_3-a_2a_3+a_1a_2a_3)$

特殊的数

Catalan 数

Catalan 数有三种计算公式

公式 $1$：

$C_n = \frac{1}{n + 1}\tbinom{2n}{n}=\tbinom{2n}{n}-\tbinom{2n}{n+1}=\tbinom{2n}{n}-\tbinom{2n}{n-1}$

公式 $1$ 可以从一个基本模型推导出来：把 $n$ 个 $1$ 和 $n$ 个 $0$ 排成一行，使这一行的任意 $k$ 个数中 $1$ 的数量总是大于或等于 $0$ 的数量，这样的排列一共有 $C_n$ 个

公式 $2$：

$C_n=\sum\limits_{k=0}^nC_kC_{n-1-k},\ C_0 = 1$

公式 $3$：

$C_n=\frac{4n-2}{n+1}C_{n-1}$

模型 1：棋盘问题

一个 $n$ 行 $n$ 列的棋盘，从左上角走到右上角，一直在对角线右下方走，不穿过主对角线，走法有多少种？

对方向编号，向上为 $0$，向右为 $1$，那么从左下角到右上角一定会经过 $n$ 个 $1$ 和 $n$ 个 $0$，如果第 $k$ 步之前 $0$ 的个数超过 $1$ 的个数了，就说明一定超过对角线了

从左下角到右上角的路线方案总共有 $3$ 种：

• A ：在对角线下方的方案数
• B ：在对角线上方的方案数
• C ：穿过对角线的方案数

显然， $\tbinom{2n}{n}=A+B+C$，现在的问题转化成如何求 $B+C$

我们需要找一条穿过对角线或者完全在对角线上方的路线，然后按照一条虚线映射

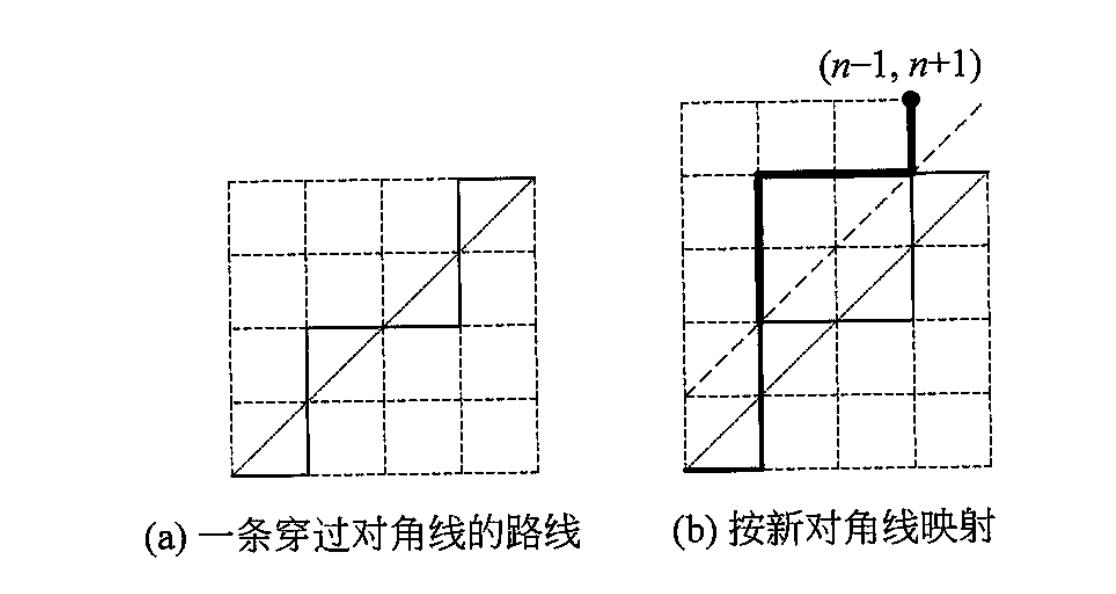
我们发现，一条穿过对角线的路线和新路线是一一对应的，而新路线的方案数是 $\tbinom{2n}{n+1}=\tbinom{2n}{n-1}$，从 $2n$ 个里面选 $n+1$ 个 $0$，选 $n-1$ 个 $1$

所以 $C_n = \tbinom{2n}{n}-\tbinom{2n}{n-1}$

使用生成函数推导

根据递推公式：

$C_n=\sum\limits_{k=0}^nC_kC_{n-1-k}$

定义生成函数 $f(x)=\sum\limits_{n=0}^{\infty}C_nx^n$，那么：

$\begin{aligned} C(x)&=\sum\limits_{n\ge 0} C_nx^n\\ &=1+x+x\sum\limits_{n\ge 1} \sum\limits_{i=0}^nC_iC_{n-1}x^n\\ &=1+x+x(C(x)^2-1)\\ &=1+xC^2(x) \end{aligned}$

考虑类似于实数的二次方程，解得：

$C(x)=\frac{-1+\sqrt{1-4x}}{2x}$

其中：

$\begin{aligned} (1-4x)^{\frac{1}{2}}&=\sum_{n=0}^{\infty} \binom{\frac{1}{2}}{n}(-4)^nx^n\\ &=\sum\limits_{n\ge 0}\frac{\frac{1}{2}(\frac{1}{2}-1)(\frac{1}{2}-2)\cdots(\frac{1}{2}-n+1)}{n!}(-4)^nx^n \end{aligned}$

所以：

$C(x)=-\sum\limits_{n\ge 0}\frac{\frac{1}{2}(\frac{1}{2}-1)(\frac{1}{2}-2)\cdots(\frac{1}{2}-n)}{(n+1)!}(-4)^nx^n$

$\begin{aligned} [x^n]C(x)&=\frac{\frac{1}{2}(\frac{1}{2}-1)(\frac{1}{2}-2)\cdots(\frac{1}{2}-n)}{(n+1)!}(-4)^n\\ &=-\frac{\frac{1}{2}(-\frac{1}{2})(-\frac{3}{2})\cdots(-\frac{2n-1}{2})\cdot1\cdot2\cdots n}{(n+1)!(n)!}(-4)^n\\ &=\frac{1\cdot3\cdot5\cdots2n-1\cdot2\cdot4\cdots2n}{(n+1)!n!}\\ &=\frac{(2n)!}{(n+1)!n!}=\frac{1}{n+1}\binom{2n}{n} \end{aligned}$

斯特林数

第二类斯特林数

考虑一个问题：

有 $n$ 个互不相同的求球，放到 $k$ 个互不区分的盒子里，每个盒子里至少要有一个球，球方案数

用动态规划来解决这个问题

$f(n,k)=kf(n-1,k)+f(n-1,k-1)$

我们定义 $f(n,k)$ 为第二类斯特林数，记作 $S_2(n,k)$，这种方法的时间复杂度为 $O(nk)$

考虑用容斥原理求出 $O(k\log n)$ 的递推式

先把盒子按照 $1\sim k$ 编号，设 $a_i$ 表示第 $i$ 个盒子没有球，答案就是

$N((1-a_1)\cdots(1-a_k))=\sum\limits_{i=0}^k(-1)^i\binom{k}{i}(k-i)^n=S_2(n,k)\times k!$

则我们能得到第二类斯特林数的通项公式

${n\brace k}=\frac{1}{k!}\sum\limits_{i=0}^k(-1)^i\binom{k}{i}(k-i)^n$

第二类斯特林数还有一个重要的公式

$n^m=\sum\limits_{k=0}^m {m\brace k} n^{\underline{k}}$

可以思考组合意义来理解，把 $m$ 个相互区分的球放到 $n$ 个相互区分盒子里面，朴素的方法就是 $n^m$

我们可以先去 $k$ 个盒子放球，要求每个盒子中至少有一个球，这个的方案数就是 $C_n^kS_2(m,k)k!=S_2(m,k)n^{\underline{k}}$

第二类斯特林数有关于 $n$ 的指数生成函数

$\sum_{n\ge 0} S_2(n,k)\frac{x^n}{n!}=\frac{1}{k!}(\exp(x)-1)^k$

这样就可以求一行的斯特林数，就是 $n$ 固定

我们有

${n\brace k}=\frac{1}{k!}\sum_{i=0}^k(-1)^i\binom{k}{i}(k-i)^n=\sum_{i=0}^k(-1)^i\frac{1}{i!}\times \frac{1}{(k-i)!}(k-1)^n$

设 $f(x)=\sum_{i=0}^n(-1)^i\frac{1}{i!}x^i,g(x)=\sum_{j=0}^n\frac{1}{j!} j^n$

所以

${n\brace k}=[x^k]f(x)\cdot g(x)$

总时间复杂度为 $O(n\log n)$

分拆数

$n$ 个无标号的球分配到 $k$ 和无标号的盒子的方案数，每个盒子不为空，记为 $p(n,k)$

有递推关系

$p(n,k)=p(n-1,k-1)+p(n-k,k)$

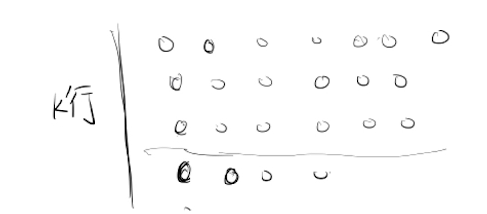
构造一种排列方式，一共有 $k$ 行，每一行的球的数量都比上一行少，每一列考虑：

• 如果最后一行只有一个球 $p(n-1,k-1)$
• 如果最后一行不止一个球 $p(n-k,k)$

关于 $n$ 的常生成函数：$\sum_{n\ge 0}p(n,k)x^n=x^k\prod_{i=1}^k \frac{1}{1-x^i}$

如何快速求 $p(n,k)$：先取 ln 再 exp

$n$ 个无标号的球分配到一些无编号盒子，每个盒子不为空的方案数，记为 $p(n)$

有 $p(n)=\sum_{k=1}^n p(n,k)$

递推关系

$p(n)=\sum_{k\ge 1}(-1)^{k-1}(p(n-\frac{3k^2-k}{2})+p(n-\frac{3k^2+k}{2}))$

常生成函数

$\sum_{n\ge 0} p(n) x^n=\prod_{i\ge 1}\frac{1}{1-x^i}$

这个表展示了一些经典的分配问题