 AtCoder Beginner Contest 353 A-G 题解
AtCoder Beginner Contest 353 A-G 题解
AtCoder Beginner Contest 353 (opens new window)
# A - Buildings
# Solution
纯模拟
# Code
#include <bits/stdc++.h>
using namespace std;
int main() {
int n; cin >> n;
vector<int> a(n + 1);
int pos = -1;
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 2; i <= n; i++)
if (a[i] > a[1]) {
pos = i;
break;
}
cout << pos << endl;
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# B - AtCoder Amusement Park
# Solution
使用两个指针模拟
# Code
#include <bits/stdc++.h>
using namespace std;
int main() {
int ans = 0;
int n, k; cin >> n >> k;
vector<int> a(n + 1);
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 1; i <= n;) {
int sum = 0;
int j = i;
while (j <= n && sum + a[j] <= k) sum += a[j++];
ans += 1;
i = j;
}
cout << ans << endl;
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# C - Sigma Problem
# Question
C - Sigma Problem (opens new window)
对于正整数 和 ,定义 为
给定一个长度为 的序列 计算:
# Solution
的最大值是 所以如果 最大为
所以对于
我们对于每个 只需要求出有多少 对于 排序后, 从小到大枚举,分界点从大变小,可以用双指针来实现
# D - Another Sigma Problem
# Question
定义 表示把两个十进制接起来
例如
给定数组 ,求:
# Solution
化简
# Code
#include <bits/stdc++.h>
using namespace std;
int main() {
int ans = 0;
int n, k; cin >> n >> k;
vector<int> a(n + 1);
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 1; i <= n;) {
int sum = 0;
int j = i;
while (j <= n && sum + a[j] <= k) sum += a[j++];
ans += 1;
i = j;
}
cout << ans << endl;
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# E - Yet Another Sigma Problem
# Question
对于字符串 和 ,定义 如下:
- 是 和 的最长公共前缀的长度。
给你一个由小写英文字母组成的 字符串 求:
# Solution
字典树板子题
# Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
const int maxn = 3e5 + 10;
int cnt;
struct Node {
int val;
int son[26];
Node() {
val = 0;
memset (son, 0, sizeof (son));
}
}tr[maxn];
void insert (string s) {
int p = 0;
for (int i = 0; i < s.size(); i++) {
int u = s[i] - 'a';
if (!tr[p].son[u]) tr[p].son[u] = ++cnt;
p = tr[p].son[u];
tr[p].val += 1;
}
}
int find_same (string s) {
int p = 0;
int res = 0;
for (int i = 0; i < s.size(); i++) {
int u = s[i] - 'a';
if (!tr[p].son[u]) break;
p = tr[p].son[u];
res += tr[p].val;
}
return res;
}
signed main() {
// freopen ("E.in", "r", stdin);
int n; cin >> n;
ll ans = 0;
for (int i = 1; i <= n; i++) {
string s; cin >> s;
ans += find_same (s);
insert (s);
}
cout << ans << endl;
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
# F - Tile Distance
# Question
F - Tile Distance (opens new window)
坐标平面上有两种类型的瓷砖,大小为 和大小为
交替铺设,穿过一个瓷砖的代价为
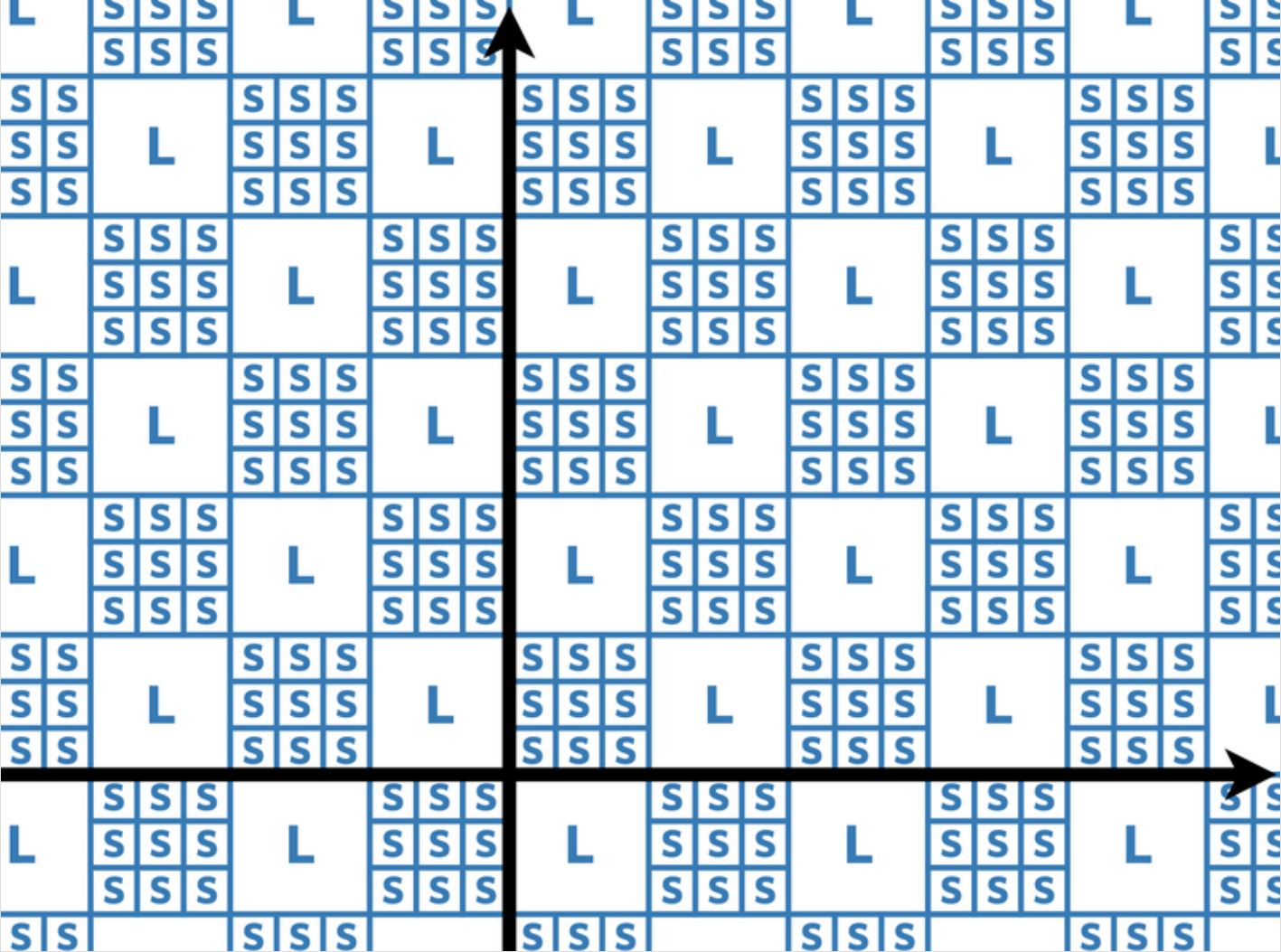
问高桥从点 移动到点 的最小代价
# Solution
显然,能走大格子就走大格子
如果起点和终点在小格子中,先走到附近的大格子里面,然后查询大格子之间的最短路径,一共有 条
# Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
ll K; cin >> K;
ll Sx, Sy, Tx, Ty; cin >> Sx >> Sy >> Tx >> Ty; Sx += K, Sy += K, Tx += K, Ty += K;
ll dist = abs(Tx - Sx) + abs(Ty - Sy);
if (1 < K) {
vector<tuple<ll, ll, ll> > st;
if (((Sx / K) ^ (Sy / K)) & 1) {
st.emplace_back(Sx / K, Sy / K, 0);
}
else {
st.emplace_back(Sx / K - 1, Sy / K, 1 + Sx % K);
st.emplace_back(Sx / K + 1, Sy / K, K - Sx % K);
st.emplace_back(Sx / K, Sy / K - 1, 1 + Sy % K);
st.emplace_back(Sx / K, Sy / K + 1, K - Sy % K);
}
vector<tuple<ll, ll, ll> > ed;
if (((Tx / K) ^ (Ty / K)) & 1) {
ed.emplace_back(Tx / K, Ty / K, 0);
}
else {
ed.emplace_back(Tx / K - 1, Ty / K, 1 + Tx % K);
ed.emplace_back(Tx / K + 1, Ty / K, K - Tx % K);
ed.emplace_back(Tx / K, Ty / K - 1, 1 + Ty % K);
ed.emplace_back(Tx / K, Ty / K + 1, K - Ty % K);
}
if (K == 2) {
for (auto [sx, sy, d1] : st)
for (auto [tx, ty, d2] : ed)
dist = min(dist, abs(sx - tx) + abs(sy - ty) + abs (abs(sx - tx) - abs(sy - ty)) / 2 + d1 + d2);
}
else {
for (auto [sx, sy, d1] : st)
for (auto [tx, ty, d2] : ed)
dist = min(dist, abs(sx - tx) + abs(sy - ty) + abs(abs(sx - tx) - abs(sy - ty)) + d1 + d2);
}
}
cout << dist << endl;
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
# G - Merchant Takahashi
# Question
AtCoder 王国有 个城镇:城镇 、 、 、 。从 镇到 镇,必须支付 日元的过路费。
商人高桥正在考虑参加 个或更多即将到来的市场。
第 个市场 由一对整数 描述,其中市场在城镇 举行,如果他参加,将赚取 日元。
对于所有的 , 次市场在 次市场开始之前结束。他移动的时间可以忽略不计。
他从 日元开始,最初在 镇。通过优化选择参与哪些市场以及如何移动,确定他可以获得的最大利润。
从形式上看,如果他在 个市场后获得最大资金额,那么 就是他的最终资金额。求 。
# Solution
显然 DP
定义 表示第 个活动结束后,且第 个活动必须参加所能达到的最大钱数
那么
我们可以根据 和 的大小分类讨论
- 时
- 时
用两棵线段树维护就好了
# Code
#include <bits/stdc++.h>
using namespace std;
typedef __int128 ll;
const ll inf = 1e18;
const ll INF = inf * inf;
ll read() {
ll x = 0, f = 1; char ch = getchar();
while (!isdigit(ch)) {if (ch == '-') f = -1; ch = getchar();}
while (isdigit(ch)) {x = x * 10 + ch - '0'; ch = getchar();}
return x * f;
}
void print(ll x) {
if (x < 0) {putchar('-'); x = -x;}
if (x > 9) print(x / 10);
putchar(x % 10 + '0');
}
struct Segment_Tree {
vector<ll> val;
int n;
Segment_Tree(int n) : n(n) {val.assign(4 * n, -INF);}
void push_up(int x) {val[x] = max(val[x << 1], val[x << 1 | 1]);}
ll query(int x, int l, int r, int ql, int qr) {
if (ql <= l && r <= qr) return val[x];
if (ql > qr) return -INF;
ll res = -INF;
int mid = (l + r) / 2;
if (ql <= mid) res = max(res, query(x << 1, l, mid, ql, qr));
if (qr > mid) res = max(res, query(x << 1 | 1, mid + 1, r, ql, qr));
return res;
}
void update(int x, int l, int r, int pos, ll v) {
if (l == r) {val[x] = v; return;}
int mid = (l + r) / 2;
if (pos <= mid) update(x << 1, l, mid, pos, v);
else update(x << 1 | 1, mid + 1, r, pos, v);
push_up(x);
}
};
int main() {
ll ret = 0;
int n; cin >> n;
ll C = read();
int m; cin >> m;
vector<ll> T(m + 1, 0ll), P(m + 1, 0ll);
for (int i = 1; i <= m; i++)
T[i] = read(), P[i] = read();
Segment_Tree up(n + 1), dn(n + 1);
up.update(1, 1, n, 1, C);
dn.update(1, 1, n, 1, -C);
vector<ll> dp(n + 1, -INF); dp[1] = 0;
for (int i = 1; i <= m; i++) {
ll ans_l = up.query(1, 1, n, 1, T[i] - 1) - C * T[i] + P[i];
ll ans_r = dn.query(1, 1, n, T[i] + 1, n) + C * T[i] + P[i];
ll ans = max(ans_l, ans_r);
ans = max(ans , dp[T[i]] + P[i]);
dp[T[i]] = max(dp[T[i]], ans);
ret = max(ret, ans);
up.update(1, 1, n, T[i], ans + C * T[i]);
dn.update(1, 1, n, T[i], ans - C * T[i]);
}
print(ret); puts("");
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
