分块

算法思想

分块不是一种数据结构，而是一种思想

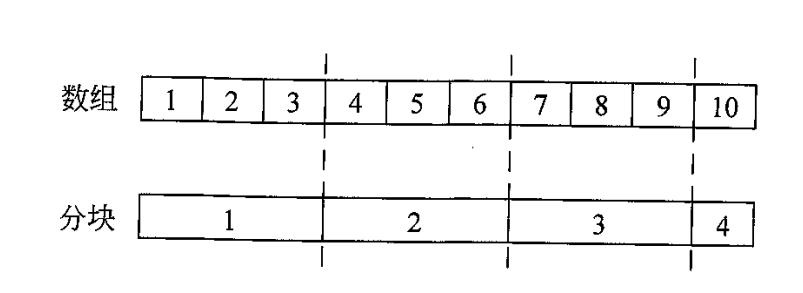
通过对原数据的适当划分，并在划分后的每一个块上预处理部分信息，从而较一般的暴力算法取得更优的时间复杂度。

实现

具体来说分块的基本要素如下：

1. 块的大小：$block$，一般情况下都定义 $block=\sqrt{n}$
2. 块的数量：$num$
3. 块的左右边界，定义数组 $st,ed$，分别表示第 $i$ 个块的第一个和最后一个元素的位置，显然有 $st[1]=1,ed[1]=block,st[2]=block+1,ed[2]=2\times block,st[i]=(i-1)\times block+1,ed[i]=i\times block$
4. 每个元素属于的块 $belong[i]$ 表示第 $i$ 个元素所在的块，有 $belong[i]=(i-1)/block+1$

下面是常见分块代码实现

    int block = sqrt(n), t = n / block + (n % block != 0); // t 表示块数
    for (int i = 1; i <= t; i++)
        st[i] = (i - 1) * block + 1, ed[i] = i * block;
    ed[t] = n;
    for (int i = 1; i <= n; i++)
        belong[i] = (i - 1) / block + 1;

用分块解决区间问题很方便，定义区间有关的数组，

例如我们需要求区间和，就定义 $sum[i]$ 表示第 $i$ 个块的 $a$ 的和，并预处理出初始值

for (int i = 1; i <= num; i++)
        for (int j = st[i]; j <= ed[i]; j++)
            sum[j] += a[j];

然后 $add[i]$ 表示第 $i$ 个块的增量标记，初始为 $0$

考虑区间修改：将 $[L,R]$ 内每个数加上 $d$

• 如果区间 $[L,R]$ 在某个块内，直接暴力修改，然后更新 $sum[i]=sum[i]+d(R-L+1)$，计算次数为 $n/t$
• 如果跨越了多个块，假设被 $[L,R]$ 包含了 $k$ 个块，更新 $add[i]+=d$ 对于两头没有完全包含的就暴力处理，计算次数为 $n/t+k$

考虑区间查询：输出 $[L,R]$ 内每个数的和

• 区间 $[L,R]$ 在一个块内，暴力累计，最后加上 $add[i]$ ，答案就是 $\sum\limits_{i=L}^R a_i+add[i]\times (R-L+1)$，计算次数为 $n/t$
• 区间 $[L,R]$ 跨越了多个块，在被 $[L,R]$ 那些完全包含的块内，$and+=sum[i]+add[i]\times len[i]$，两头的情况暴力处理 ，计算次数为 $n/t+k$

所以块的大小 $block$ 为多少时最优，每次操作的次数为 $n/t+k$ 或 $n/t$，$k$ 最大 $=t$，最差时间复杂度为 $O(n/t+t)$ 按照基本不等式 $t=\sqrt{n}$ 时最优，此时 $block=n/t=\sqrt{n}$