 半平面交
半平面交
# 半平面交
半平面交就是给出若干个半平面,求他们的公共部分。
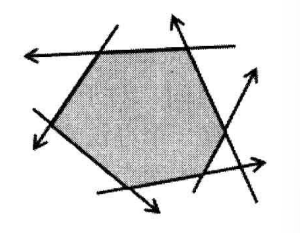
显然,半平面交肯定是一个凸的东西,也可能为空
求半平面交也可以使用类似于凸包的算法在 的时间复杂度内解决,不同的是凸包使用的是栈,半平面交使用的是双端队列
按照极角排序后,每次新加入的半平面可能会让队尾的半平面变得"无用",从而需要删除
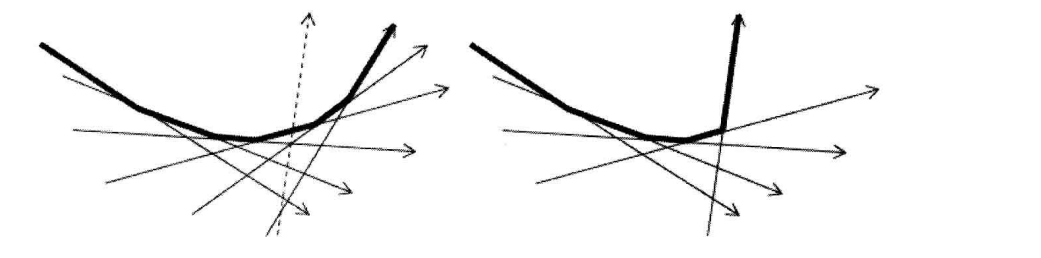
注意,新加的半平面也有可能“绕了一圈”以后让队首的半平面变得无用
bool on_left(const Line &L, const Point &P) { return cross(L.v, P - L.P) > 0; } //点 p 在有向直线 L 的左边(线上不算)
int half_plan_intersection (vector<Line> L, vector<Point> &poly) {
int n = L.size();
sort(L.begin(), L.end(), [](const Line &a, const Line &b) {
return angle0(a.v) < angle0(b.v); // 按极角排序
});
int first, last;
vector<Point> p(n);
vector<Line> q(n);
q[first = last = 0] = L[0];
for (int i = 1; i < n; i++) {
while (first < last && !on_left(L[i], p[last - 1])) last--;
while (first < last && !on_left(L[i], p[first])) first++;
q[++last] = L[i];
if (dcmp(cross(q[last].v, q[last - 1].v)) == 0) {
last--;
if (on_left(q[last], L[i].P)) q[last] = L[i];
}
if (first < last) p[last - 1] = line_intersection(q[last - 1], q[last]);
}
while (first < last && !on_left(q[first], p[last - 1])) last--;
if (last - first <= 1) return 0;
p[last] = line_intersection(q[last], q[first]);
int m = 0;
for (int i = first; i <= last; i++) poly[m++] = p[i];
return m;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
上次更新: 2025/04/08, 18:03:31
